在 cpp2017 大会上，google 向我们展示了 swiss tables，一种在使用性能上可以远超 std::unordered_map 的哈希表。

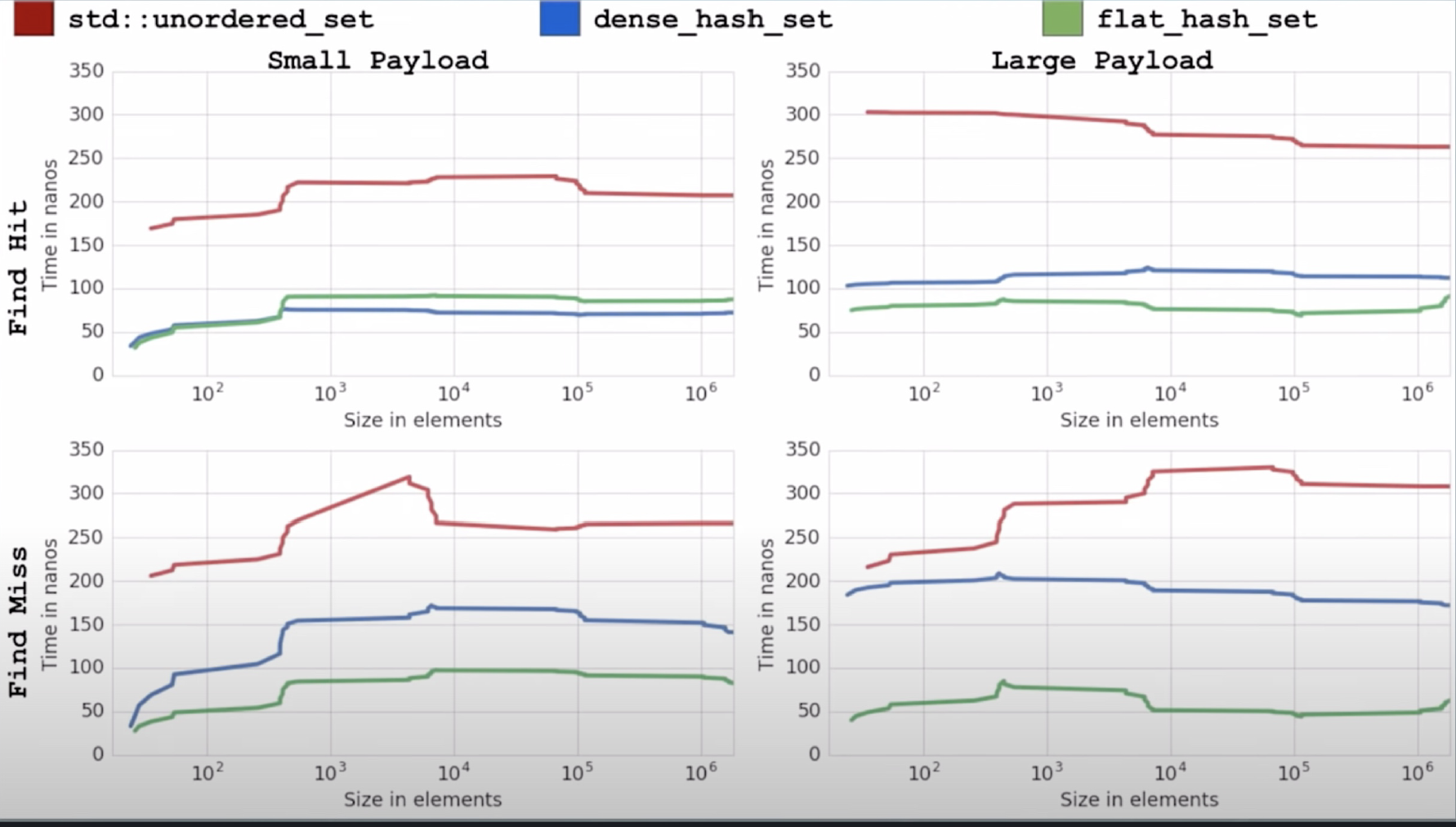
先看测试效果对比，红色的是 stl 的哈希表，蓝色的是 google 初代的哈希表，绿色的正是 swiss table，不论是在小型工程，还是大型工程，对缓存是否命中，swiss table 都有更少的耗时。

本文分为两部分，第一部分讲 c++ stl 哈希表的实现，第二部分讲 swiss tables 如何对其进行优化。

本文大纲如下：
1、Hashmap
1.1、Load factor
1.2、std::unordered_set
1.2.1、遍历操作
2、优化
2.1、如何处理哈希冲突
2.2、如何删除元素
2.3、Robin Hood hashing
2.3.1、example
2.3.2、advantage
2.4、Hashbrown(Swiss Table)
2.4.1、hash
2.4.2、insert
2.4.3、design
2.4.4、find
2.4.5、delete

1、Hashmap

Hashmaps use arrays as their backend. In the context of hashmaps, the array elements are called buckets or slots (I’ll be using this interchangeably). 哈希表底层使用的是数组，数组里的每一项称之为桶或插槽。

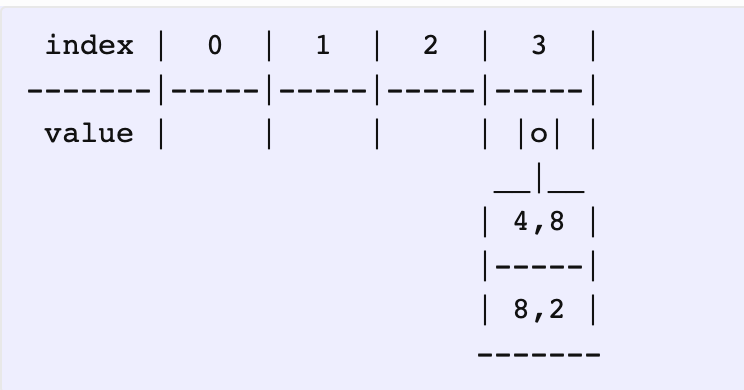
为什么要同时保存 key 和 value，因为如上图所示，是为了解决冲突，使用链表把 Hash(key) 相同的元素串起来。

1.1、Load factor

Load factor is the ratio of the number of elements in the hashmap to the number of buckets. 装载因子代表已存放的数量除以总容量。

Once we reach a certain load factor (say, 50%, 70% or 90% depending on your configuration), hashmaps will resize and rehash all the key/value pairs. 一般达到装载因子的比率时，会需要重新调整哈希表的大小，并对元素进行重新映射。

装载因子主要是进行扩容，以减少哈希碰撞。

1.2、std::unordered_set

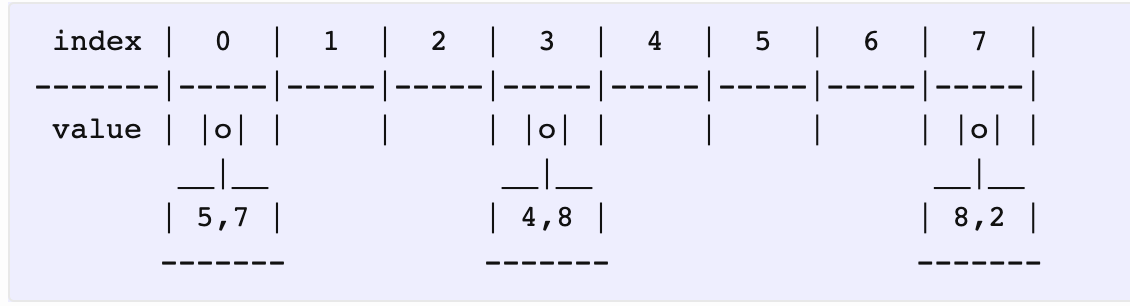
unordered_set 也是用哈希表组织的，只是存储的元素不同于 unordered_map。

同样采用的是拉链法解决冲突，存储 hash code、value 和 next 指针，一个 NULL pointer 代表链表的结束。

1.2.1、遍历操作

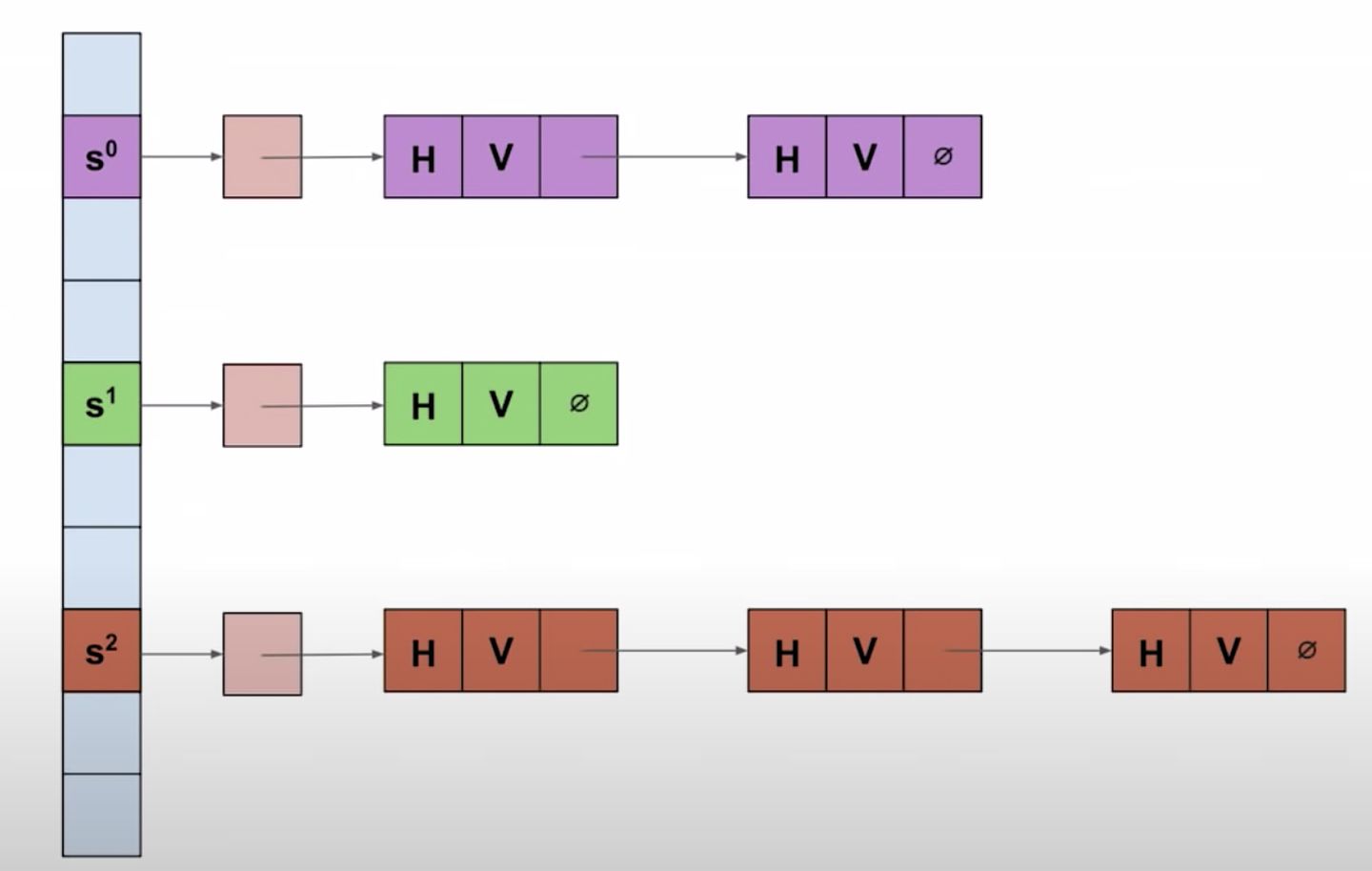
To allow optimal iteration without passing over any empty buckets, GCC’s implementation fills the buckets with iterators into a single singly-linked list holding all the values: the iterators point to the element immediately before that bucket’s elements, so the next pointer there can be rewired if erasing the bucket’s last value. 为了优化遍历操作(不会遍历空的桶)，GCC 将值用单链表的形式组织起来了。

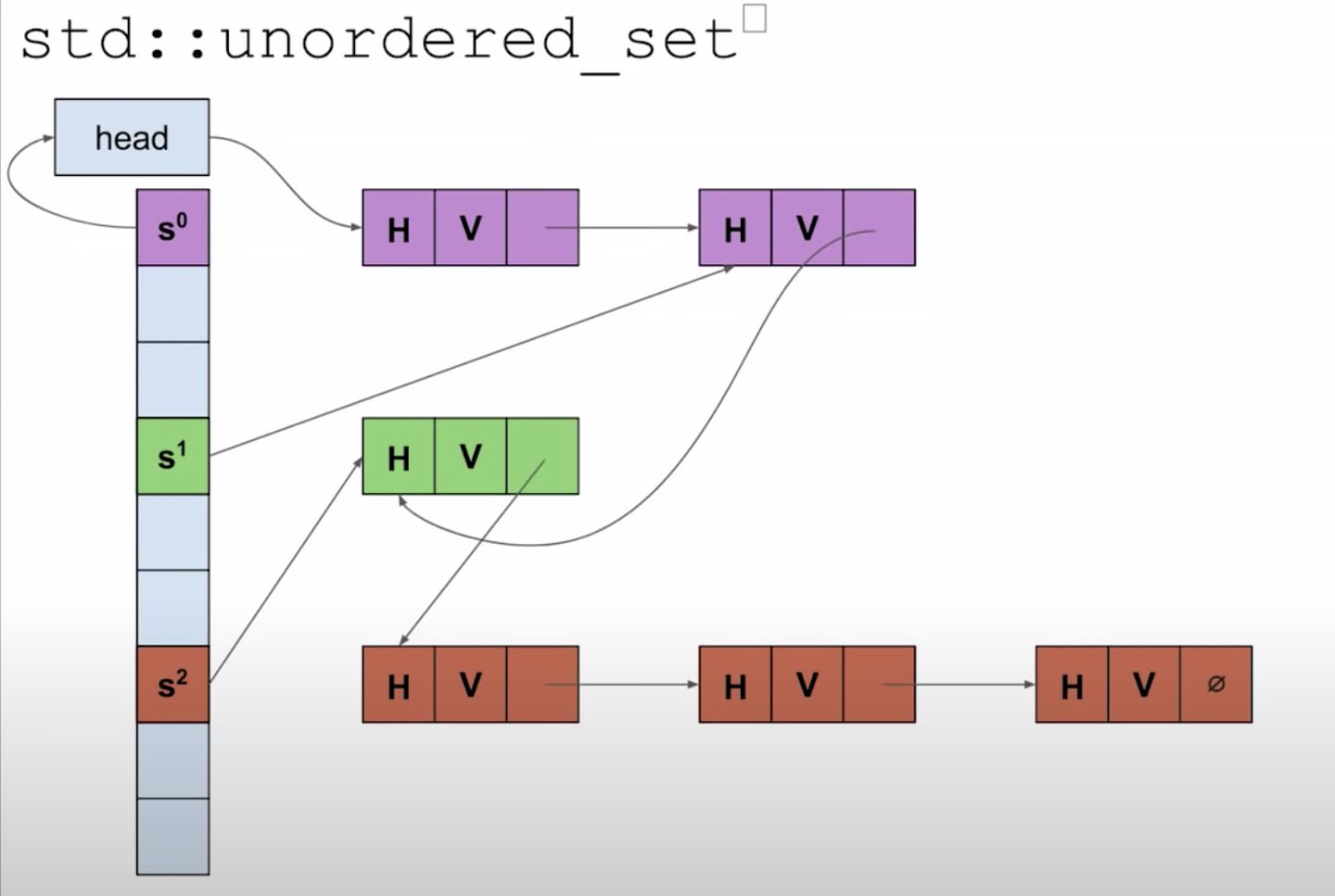
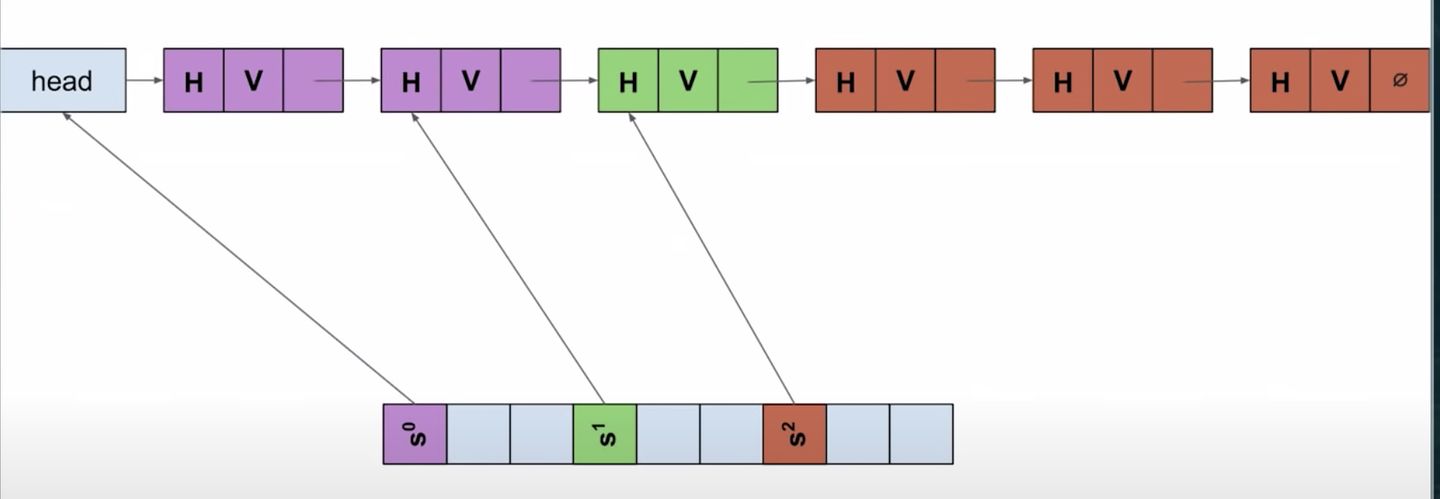
这是 GCC 对 stl 的遍历操作进行的一个优化，跳过了空桶，不同的平台或工具套件可能会有不同的优化。

2、优化

Whenever the CPU needs to read/write to a memory location, it checks the cache(s), and if it’s present, it’s a cache hit, otherwise it’s a cache miss. 如果 CPU 需要读写内存地址，会检测缓存是否存在。

Whenever a cache miss occurs, we pay the cost of fetching the data from main memory (thereby losing a few hundred CPU cycles by waiting). 如果缓存查询失败，就会有从主存加载数据的开销。

The second way (for our hashmap) is to get rid of using external data structures completely, and use the same array for storing values alongside buckets. 第二种方式是丢弃额外的数据结构，使用同一个数组来存储元素。

通过抛弃多种数据结构的实现方式，同时使用线性探测法来进行存储，对 cache 更加友好，也提高的空间局部性的利用。

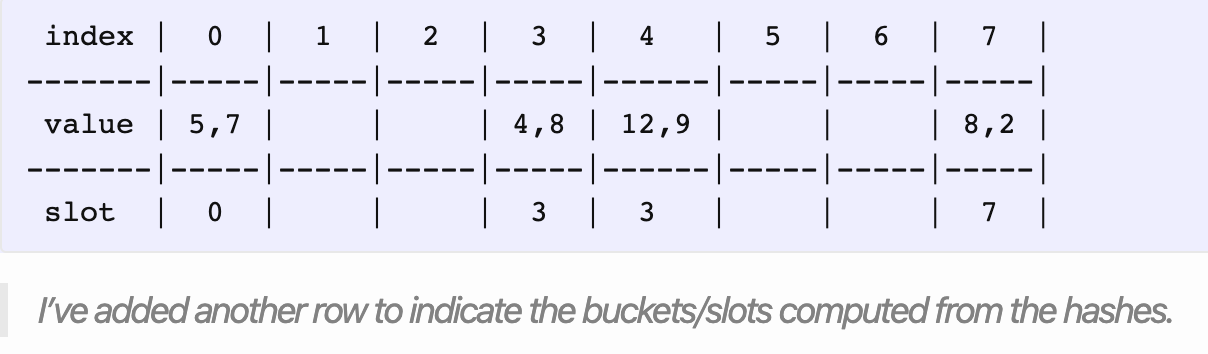
上图添加了新行表示元素计算得到的哈希值，slot 代表元素原本要插入的位置。

2.1、如何处理哈希冲突

尝试添加新的元素到数组中：

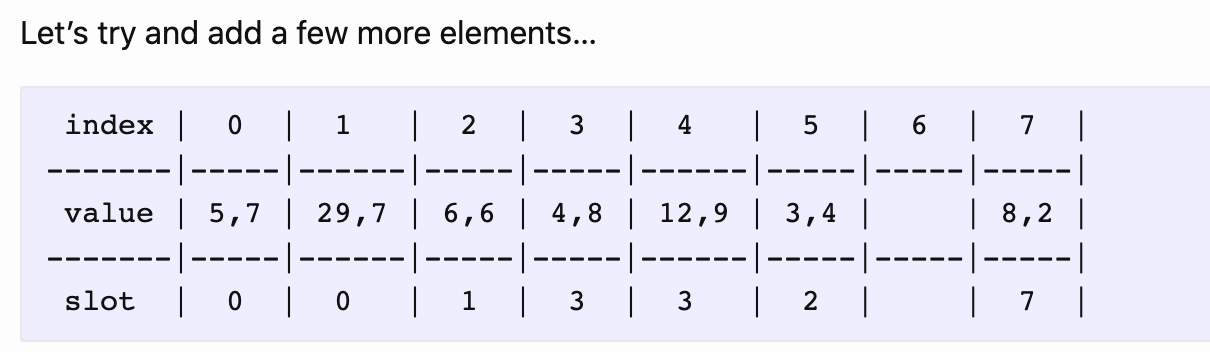
As you can see, (3, 4) has a slot index of 2, but since that index already has an element, we’re inserting it into the first empty element we find (which is at 5). During fetching, we land on a slot (based on the hash), compare the keys one by one, and traverse all the way until we either find a matching pair or an empty slot (probing).

可以看到，(3, 4) 哈希值是 2，但下标 2 的位置已经存在元素了，所以只能存到第一个空的桶(即 5)。

这里是采用线性探测法解决冲突。

The advantage of linear probing is that it has the best cache performance - if you think about it, linear probing sequentially visits the elements, which means, (most often, depending on the size of the object) the data is part of a cache line, which is great, because we don’t waste CPU cycles (in contrast, quadratic probing doesn’t offer such cache performance and double hashing uses another hash function, which by definition means that we’re spending more work on computing another hash).

线性探测法的好处是有很好的缓存表现，比如线性探测法是顺序性地访问元素，而这些连续的内存正是缓存行的一部分，省下了 CPU 指令周期。作为对比，平方探测法就没有很好的缓存表现，因为它会跳着查找。

This way, as the table grows, more elements get pushed away from their actual index (which elongages the search/probe sequence, thereby increasing the cache misses). It also depends on the hash function, in that, a weaker hash function can lead to more collisions, and hence, more clusters.

随着元素变多，这条连续的序列越来越长，会增加缓存查询失败的次数。当然这也取决于哈希算法。

2.2、如何删除元素

Here’s the catch. When you remove an element, you can’t simply remove the key/value pair from a slot and be done with it. If you do that, then you’ve created an empty slot, which could result in the map complaining existing values to be non-existent (because the search has encountered an empty slot).

当你删除元素时，由于线性探测法的查找需要，不能直接删除并置空。

So, you have two choices: 有两种操作方式

In addition to removing a pair, we also move the next pair to that slot (shift backwards). For example, if we removed (4, 8) in the above map, then we move (3, 4) to its position (which has the lowest slot index), and the table will now look like:

把后面的元素挪到要删除的元素留下的空桶，以此类推。

Or, you add a special flag (tombstone) to the removed slots, and when you probe, you skip the slots containing that flag. But, this will also affect the load factor of the hashmap - removing a number of elements in a map followed by inserting a few could trigger a rehash.

加个标记，表示元素已被删除，但这种方式会影响装载因子。

2.3、Robin Hood hashing

上面的存储方式随着元素变多，查找效率会越来越差，因为元素离它原本要插入的位置可能会越来越远。Robin Hood 哈希算法正是为了优化这种情况而设计出来的。

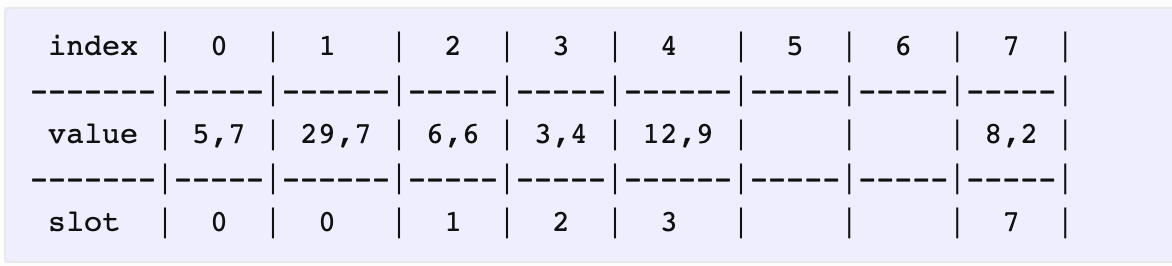
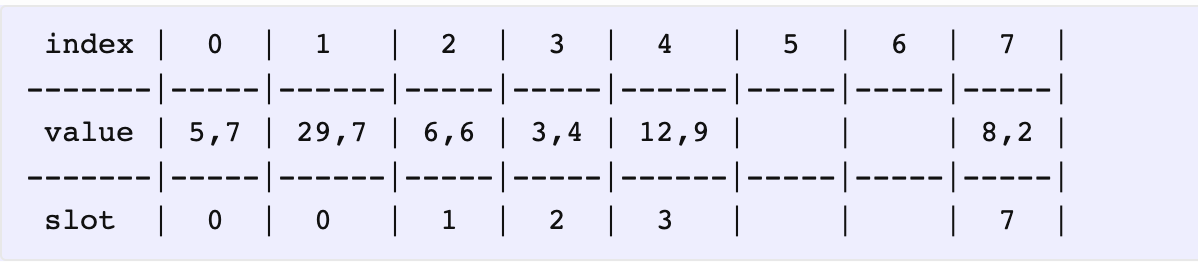
We’re interested in a variable called distance to the actual slot - I’ll call it D(value). For example, the actual slot of (5, 7) is 0, and it’s located at 0, so the distance is 0. For (29, 7) on the other hand, the distance is 1, because it’s at 1, even though it should’ve been at 0.

我们将元素的实际存放位置和它算出来的哈希值做差，称之为距离。D(value) = abs( 实际存放位置 - hash(value) )

In robin hood hashing, you follow one rule - if the distance to the actual slot of the current element in the slot is less than the distance to the actual slot of the element to be inserted, then we swap both the elements and proceed.

在新的哈希操作中，如果当前元素的距离小于要被插入元素的距离，就进行替换，并继续操作替换出来的元素插入。

2.3.1、example

We’d like to insert (13, 3) into this map. The slot index for 13 is 0. So, let’s start at 0. We already have (5, 7) located there, which also has a slot index 0.

比如插入 (13, 3)，哈希值是 0，所以从下标为 0 开始操作。下标 0 的元素距离为 0。

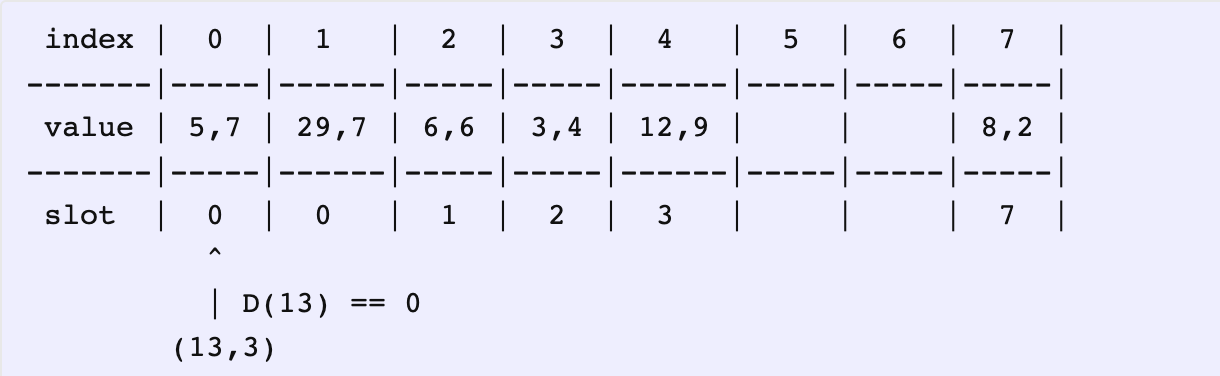
Both have the same distances i.e., D(5) == D(13) == 0. We move forward.

相等，不用替换，看下一个。

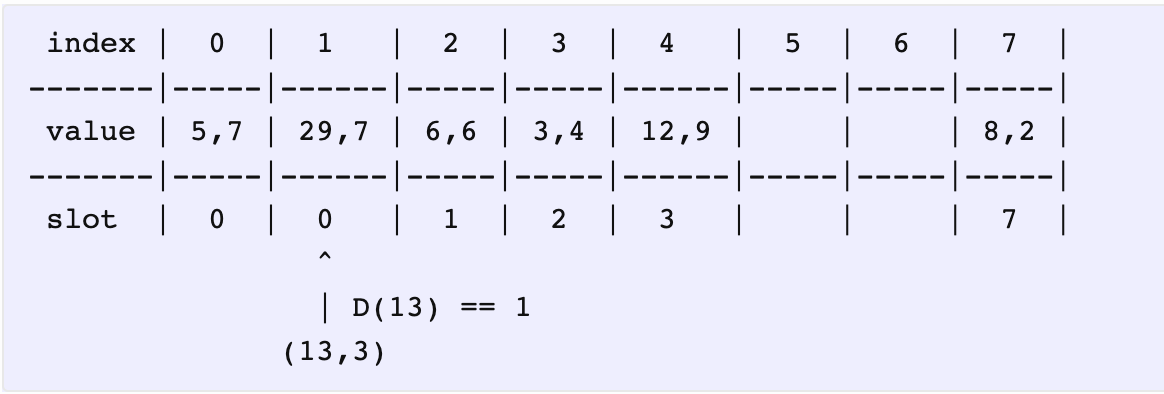
Still the same. D(29) == D(13) == 1 (both are 1 slot away from their actual slots). Moving on…

还相等，继续。

In the next stop, we see something. D(13) == 2 whereas D(6) == 1 and hence D(6) < D(13), which means we should swap the pairs and proceed.

下标 2 的元素距离更小，所以进行替换，接下来操作替换出来的元素 (6, 6)。

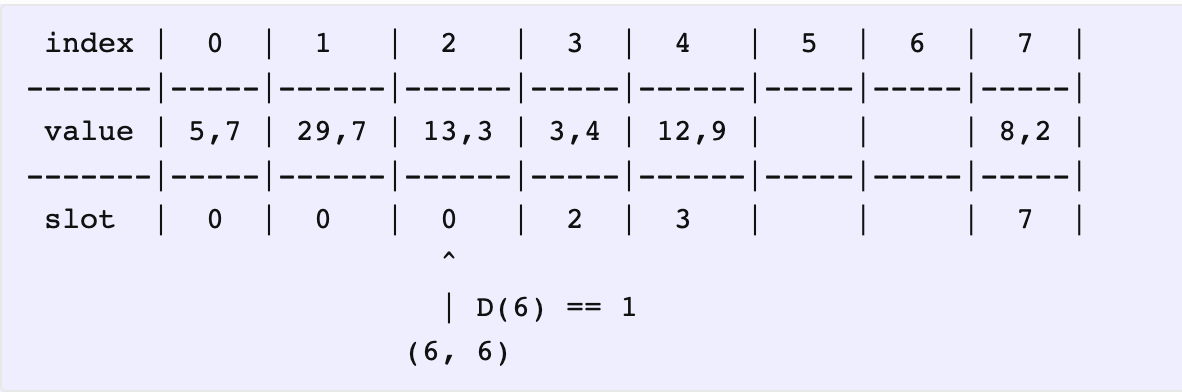
Now, we go looking for a place to insert (6, 6). This way, we compare and swap the key/value pairs based on their distances. In the end, we have this nicely distributed hashmap:

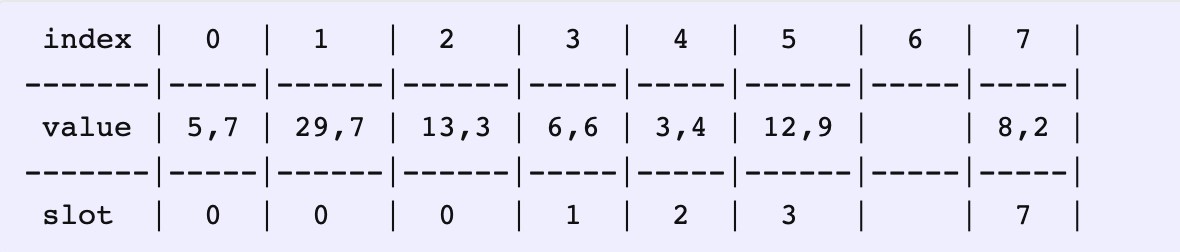
2.3.2、advantage

Since the hashmap has reached almost its capacity, you might be wondering whether this would’ve already triggered a rehash. But, the resize/rehash depends on the load factor, and because this method redistributes the key/value pairs regardless of when they get inserted (takes away from the rich and gives it to the poor, hence the name), the hashmaps could now have higher load factors of even 90-95%.

由于进行了元素位置的重新分配，所以装载因子可以设置得很高。

This also brings another improvement to searching. We don’t have to probe all the way until we find an empty slot. We can stop when D(slot value) < D(query value), since our rule guarantees that this shouldn’t happen for the key we’re looking for.

而且查找效率也变高了，不需要查询直到出现空桶为止，根据插入规则，可以直接判断距离 D(当前元素) < D(查询元素)，就能停止了，返回元素不存在。

同时也可以提供更好的空间局部性的利用。

2.4、Hashbrown(Swiss Table)

Let’s make the initial size of the internal array to WIDTH 16. We call this group of 16 elements a group. So, a map is made of a number of consecutive groups.

让我们设置初始数组大小为 16，称之为组。所以一张表是由连续的组来构成的。

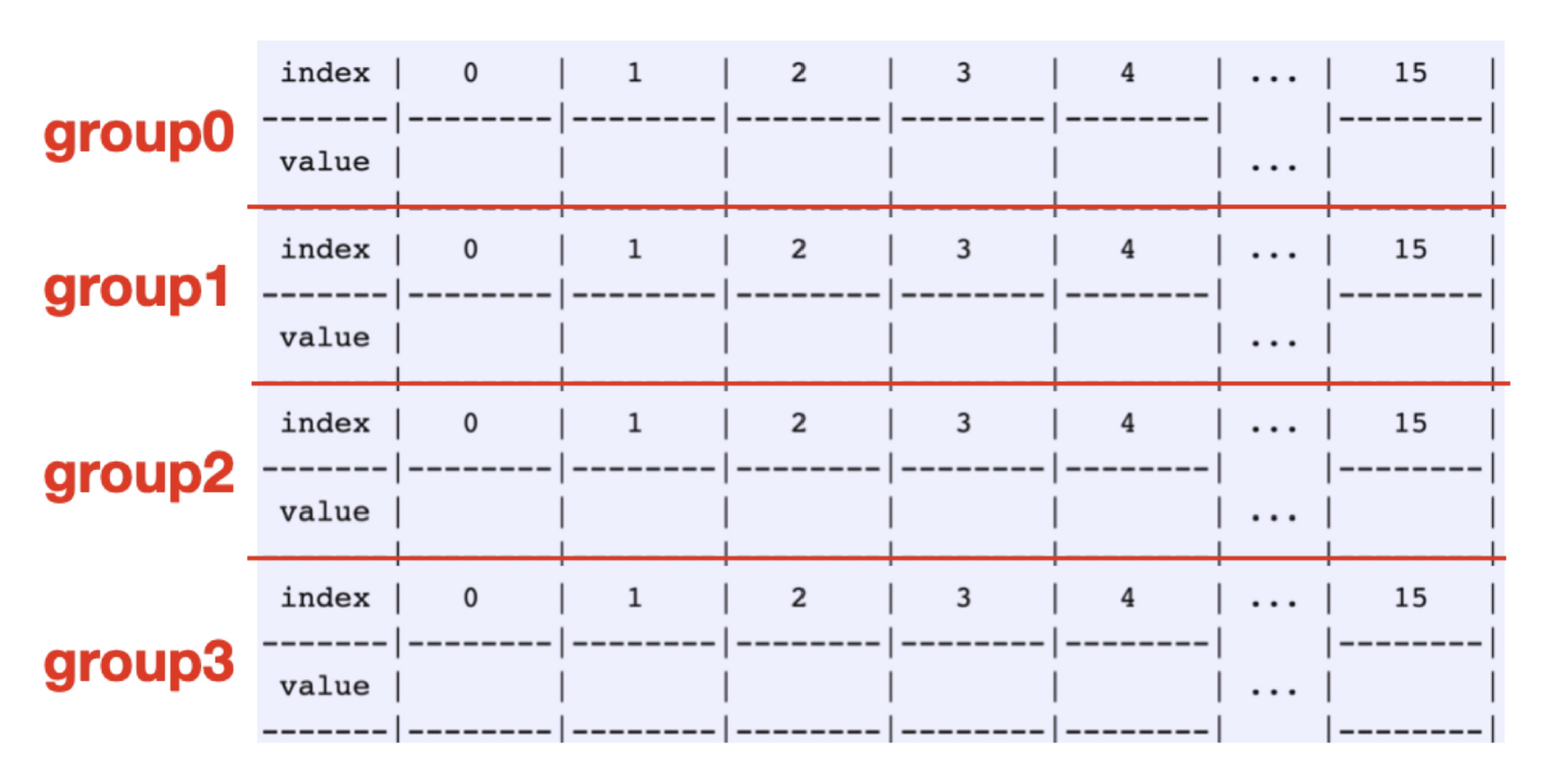
每一个组有同样的哈希值 group_index = hash(value) % num_groups，可以把一组看成拉链法里面的链表，只是这里限定为 16 个，且在内存中提前分配好了。

For each slot in a group, let’s assign a byte for metadata and call it control byte.

对于组里的每一个桶，添加一个控制信息，以一个字节来进行表示，称为控制字节。

2.4.1、hash

There are two operations we perform with a hash (I hate these names but these are the ones you’ll see in the implementations):

这里计算哈希有两个步骤

h1 - the whole hash truncated to a usize, used as an index into our array (apply modulo arithmetic to it)

h1 - 将整个哈希值截断成无符号变量，用来作为数组的下标

h2 - the top 7 bits of the hash, in FULL control byte format (see above); note that this will motivate you to have a hash function with good, uhhhhh, “entropy” in the high bits

h2 - 头 7 位作为哈希值，以控制字节的格式来使用

Our first candidate for insertion is (5, 7).

比如插入元素 (5, 7)

The absl::Hash framework is the default hash implementation for the “Swiss table” hash tables. All types hashable by the absl::Hash framework will automatically be hashable within Swiss tables.

使用这种哈希算法并不能保证安全，但能有效降低 hashmap 的冲突概率。

1

H(5) = 12638147618137026400

Taking the top (most significant) 7 bits of this hash and calling it H2(x), we get: 取头 7 位

1

H2(5) = H(5) >> 57 = 87 = 0b1010111

These will be the bottom 7 bits of our control byte. Then, we use a special bit for our own purposes (to indicate whether the slot value is empty, full or deleted) and this will be the top bit. The states are now represented as follows:

这 7 位会成为控制字节的末尾 7 位，然后控制字节的第一位会有特殊含义

1
2
3


0b11111111  // EMPTY (all bits are set)
0b10000000  // DELETED (top bit is set) (tombstone)
0b0.......  // FULL (whenever the top bit isn't set)

最高位用作特殊表示。

2.4.2、insert

Going back to our candidate (5, 7), its slot index is 0 i.e., H(5) % 16 == 0.

举例，比如插入 (5, 7)，哈希值为 0

Once the pair is inserted, we’ve also set its control byte to H2(5), since the top bit is zero anyway (because it’s now FULL). Now, let’s try inserting (39, 8).

插入之后，同时也设置好它的控制字节，首位为 0 表示桶满了，然后插入下一个元素 (39, 8)

1
2
3


H(39) = 17050702200253021726
i = H(39) % 16 = 2
H2(39) = H(39) >> 57 = 54 = 0b110110

Insertion is done in two passes 插入有两步

Pass 1: just run the search algorithm. If it returns a result, then overwrite that and return.

先使用查找算法，如果有返回，就覆盖写入

Pass 2: actual insertion (now knowing the key isn’t present, we search for EMPTY/DELETED).

无返回结果，就插入到空桶或已删除元素的桶

So, actual insertion:

start at bucket h1 (mod n) 找到哈希值对应的组
load the Group of bytes starting at the current bucket 加载组的控制字节
search the Group for EMPTY or DELETED in parallel (match_empty_or_deleted) 并行查找可插入位置
if there was no match (unlikely), probe and GOTO 2 匹配不到就线性探测下一个组，从步骤 2 再开始
otherwise, get the first match and enter the SMALL TABLE NASTY CORNER CASE ZONE 否则获取第一个匹配上的
check that the match (mod n) isn’t FULL.（This can happen for small (n < WIDTH) tables, because there are fake EMPTY bytes between us and the mirror bytes. If it does happen, then we know: we’re a tiny table that fits in a Group, and that the guaranteed-to-exist empty bucket wasn’t anywhere between h1 and the end of the table.）检查匹配的是否有元素了，因为小的表可能会有假的空控制字节，在 h1 下标及其后面，已经没有桶
if it wasn’t FULL, return that location for insertion 如果没元素，返回插入的位置
if it was FULL, load the (aligned!) Group at the start of the table 如果有，记载表开头的组
search the Group for EMPTY or DELETED in parallel (match_empty_or_deleted) 并行查找组中可插入位置
return the first location for insertion (guaranteed to exist!)

也就是说，一张表是由很多组构成的，一般插入是插入到组中对应的桶，对应桶有元素的话，就线性探测下一个组，看对应的桶，以此类推，但如果每个组对应的桶都是满的话，就加载表开头的组，并行去查找可以插入的桶。

2.4.3、design

Each group contains 16 slots summing up to 8 control bytes. 每个组都有 16 个桶，里面有 8 位的控制字节。

When we query for a key in the map, we first use the hash to land on the group corresponding to a slot, find the offset of the slot inside that group and start probing by comparing against the 7-bit hashes in the control byte.

当执行查询时，先计算出对应的桶，然后从组中拿出对应的桶，比对控制字节的后7位哈希值。

The boost here is that the control bytes (being 128 bits) can fit into an L1 cache line. This means, we can probe an entire group really quickly, before having to fetch another group from L2 or L3 or whatever. And, we don’t have to worry about comparing the keys at all, until we encounter all 7 bits matching in a control byte.

这里的加速实际上是一组的控制字节为 128 位，可以放入 L1 的缓存行，说明我们可以以很快的速度线性探测一个组，并且是在 L2 或 L3 或其他获取另一个组之前。

There’s one other cool optimization for modern processors. Modern CPUs support SIMD instructions, which basically means that we can do some operation (add or multiple or compare, etc.) on multiple values at the same time in a processor! SSE is a subset of that where we can work on different types such as two 64-bit floats, four 32-bit integers or sixteen 8-bit integers.

还有一个针对现代处理器的优化，现代 CPU 使用 SIMD 指令，可以一次操作多个值。SSE 是它的子集，可以操作其他类型，如两个 64 位浮点数，或四个 32 位整数，或十六个 8 位整数。

Now, our workflow will simply be: 所以我们的工作流可以简化如下

Load up these bytes from an array. 从一个组中加载控制字节
Set the byte to compare. 设置用于对比的字节
Compare both the values. 比对控制字节
Mask the values from comparison to true or false. 返回比较的结果

And, that’s finding the results from 16 slots in four CPU instructions!

然后我们可以通过 4 条 CPU 指令就能从 16 个桶中找到答案。

比如通过计算要查找的 key 的哈希值，得到其控制字节是 96：

首先将其展开为一组的大小，即 128 位的，16 个

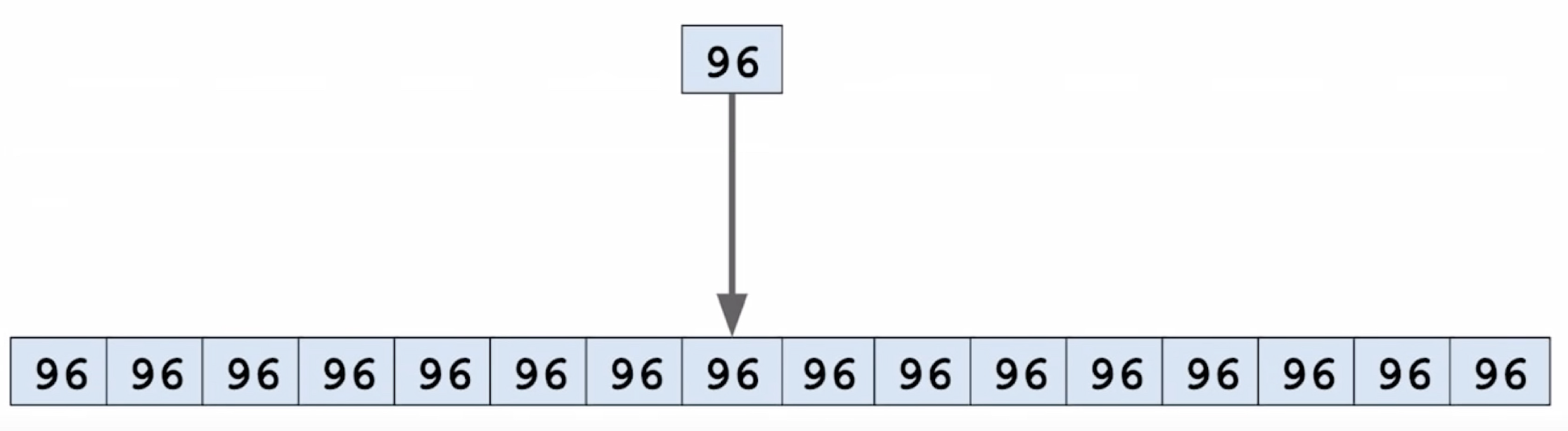
然后与对应的组的控制字节做并集

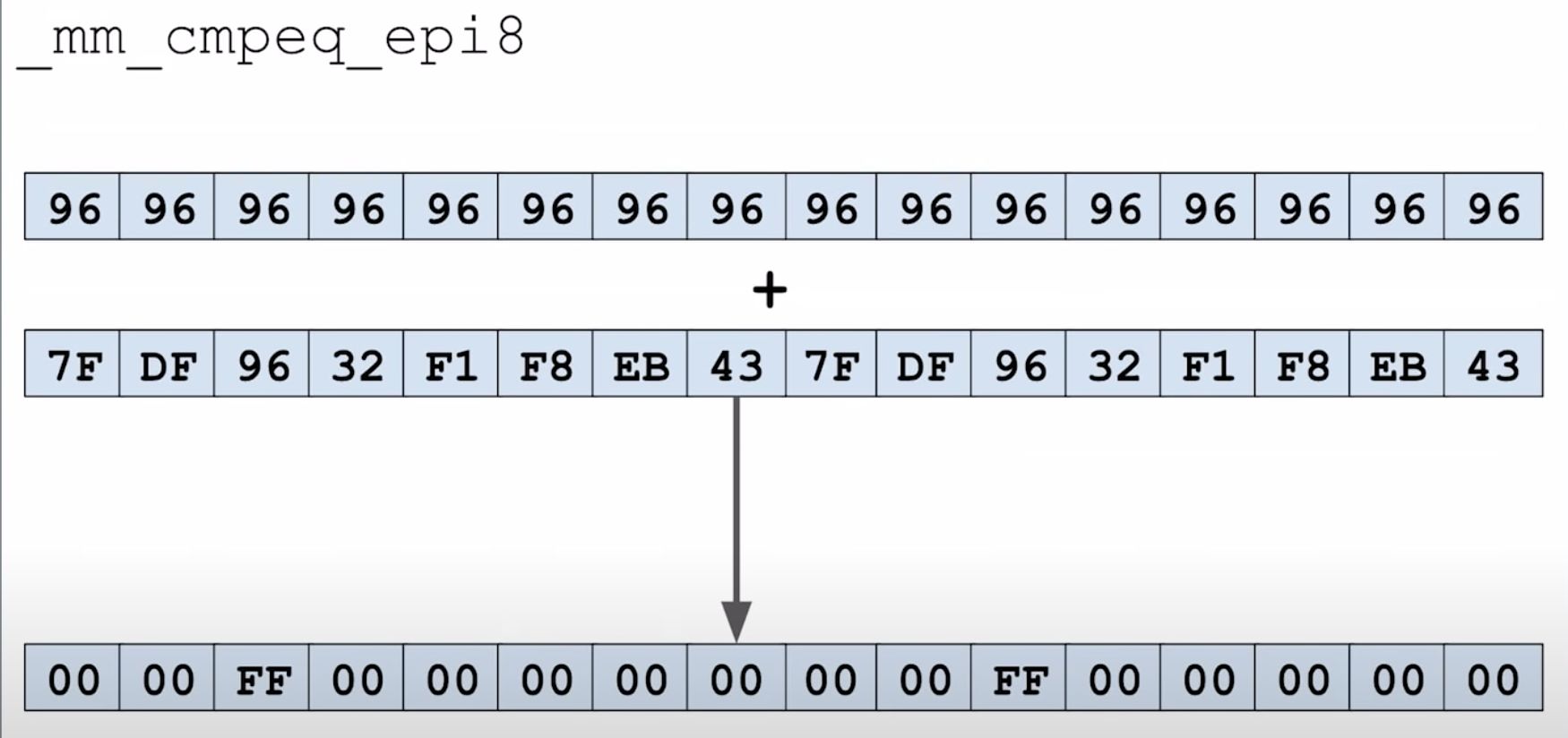
最后将结果降为 0 或 1

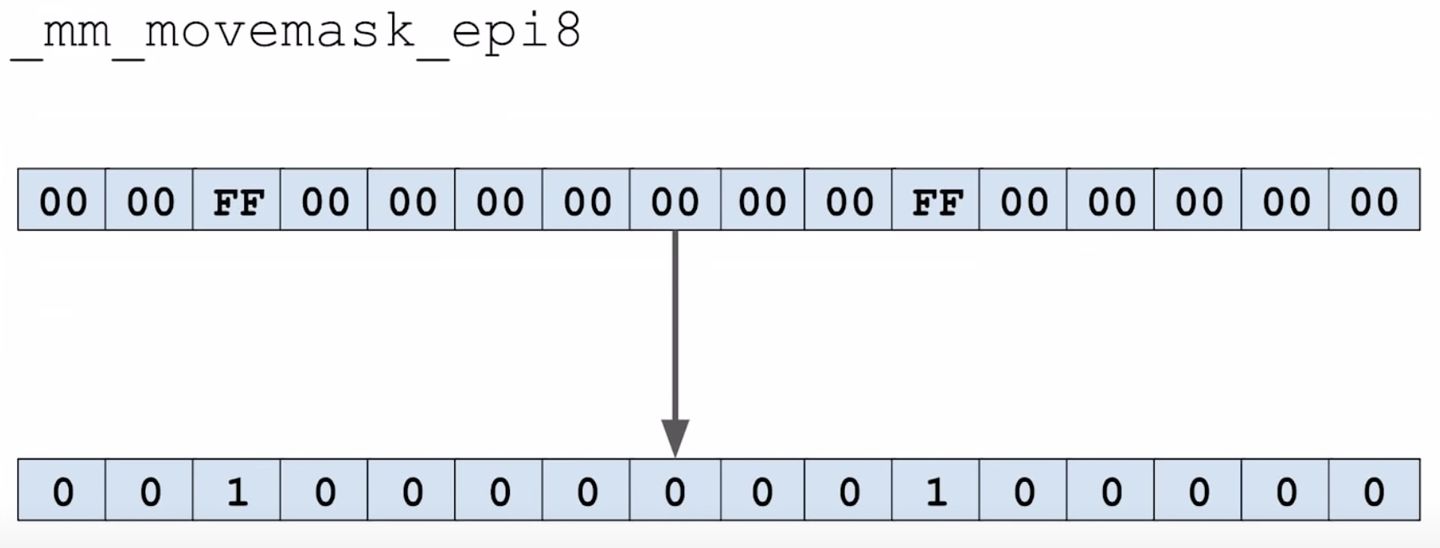
因为存在控制字节一样的情况，所以这些为 1 的元素还需要检查 key 是否真的相等。

2.4.4、find

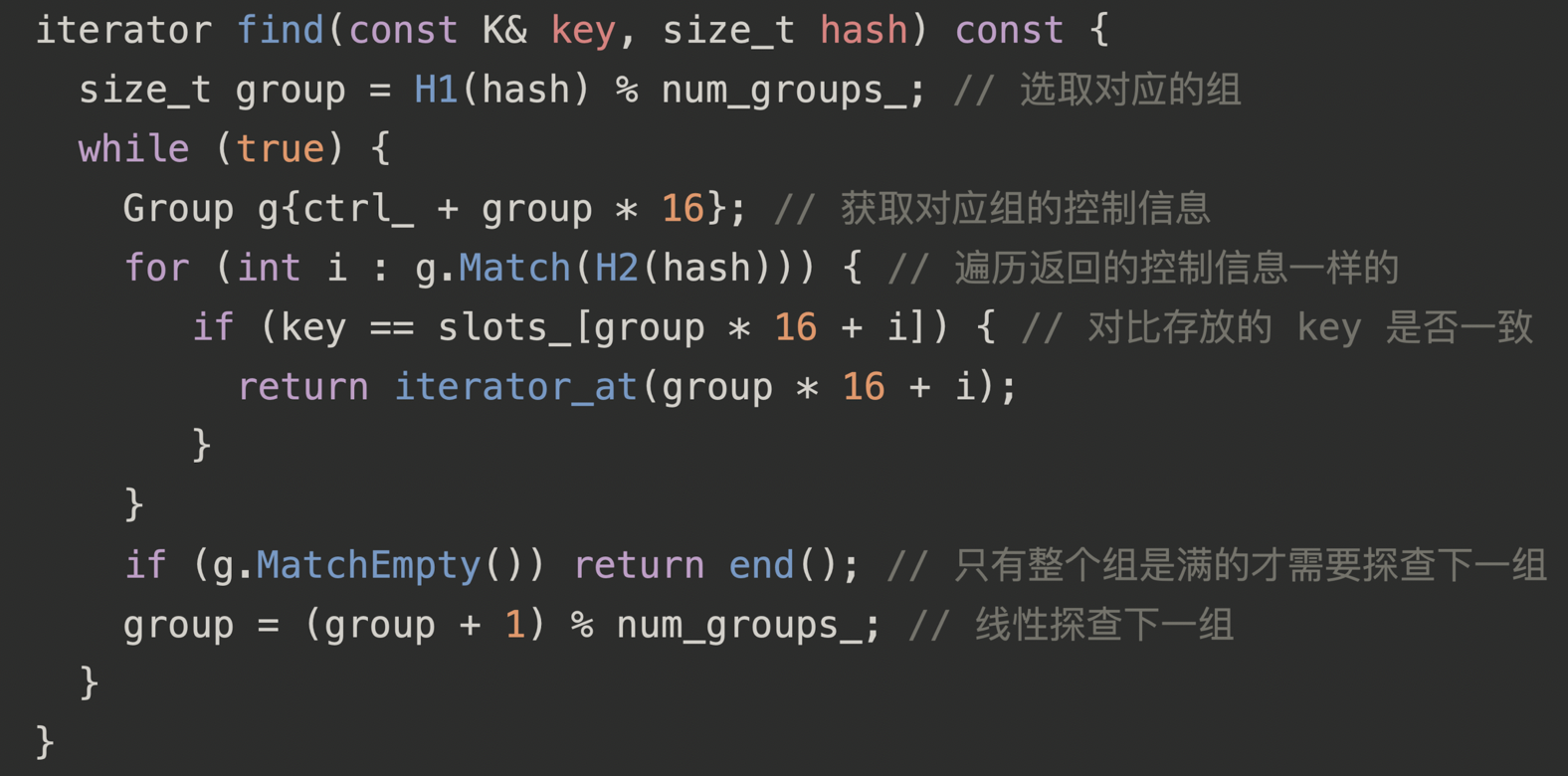
In the above example, if we wish to find 39, then all we have to do is find the position of the group using the hash, find the 7-bit value 0b110110 from the hash, and do this:

比如我们要找 39，找到组中对应的桶，计算控制字节

So, searching:

start at bucket h1 (mod n)
load the Group of bytes starting at the current bucket
search the Group for your key’s h2 in parallel (match_byte)
for each match, check if the keys are equal, return if found
search the Group for an EMPTY bucket in parallel (match_empty)
if there was any matches, return false
otherwise (every entry was FULL or DELETED), probe (mod n) and GOTO 2

Probing is done by incrementing the current bucket by a triangularly increasing multiple of Groups: jump by 1 more group every time. So first we jump by 1 group (meaning we just continue our linear scan), then 2 groups (skipping over 1 group), then 3 groups (skipping over 2 groups), and so on.

这里说的线性探测，实际上是组的纬度出发的，如果第一个组对应桶有元素了，则到下一个组看对应的桶，以此类推。

2.4.5、delete

So we saw in the searching algorithm that our cue to probe is an entire contiguous Group of FULL/DELETED entries. So if the entry we want to delete is in within such a contiguous Group, setting it to EMPTY may “break” the search path for any key that probed over it. So we need to check if that’s the case, and if so, replace ourselves with DELETED. To put that another way: we need to find the nearest EMPTYs to our left and to our right, and make sure they’re less than WIDTH apart.

查找算法是判断组中 FULL/DELETED 元素，但如果要删除的元素是在这样连续的组里的话，设置为 EMPTY 会扰乱查找算法。所以还需要进行检查，如果是，则替换为 DELEDED。需要检查的是相邻的 EMPTY，来确保这个组不是满的。

Note how extreme that is: we only ever insert a tombstone if the entry we want to delete is in a pack of WIDTH non-EMPTY buckets. Under reasonable load factors that’s very unlikely!

So, removal:

start at the removal bucket
load the Group of bytes starting at that bucket
search the Group for EMPTY in parallel (match_empty), and record the first empty found (“end”)
load the Group of bytes before that bucket
search the Group for EMPTY in parallel (match_empty), and record the last empty found (“start”)
if the distance between start and end is >= WIDTH, set the bucket to DELETED
otherwise, set the bucket to EMPTY

参考&推荐阅读

The Swiss Army Knife of Hashmaps：https://blog.waffles.space/2018/12/07/deep-dive-into-hashbrown/#fn:4

Swisstable, a Quick and Dirty Description: https://gankra.github.io/blah/hashbrown-tldr/

youtube - CppCon 2017: Matt Kulukundis “Designing a Fast, Efficient, Cache-friendly Hash Table, Step by Step”

新式哈希表 - Swiss Tables

文章目录