上篇文章介绍了 SSA，这篇文章再简单介绍下 SSA 的构造与析构。

1、案例

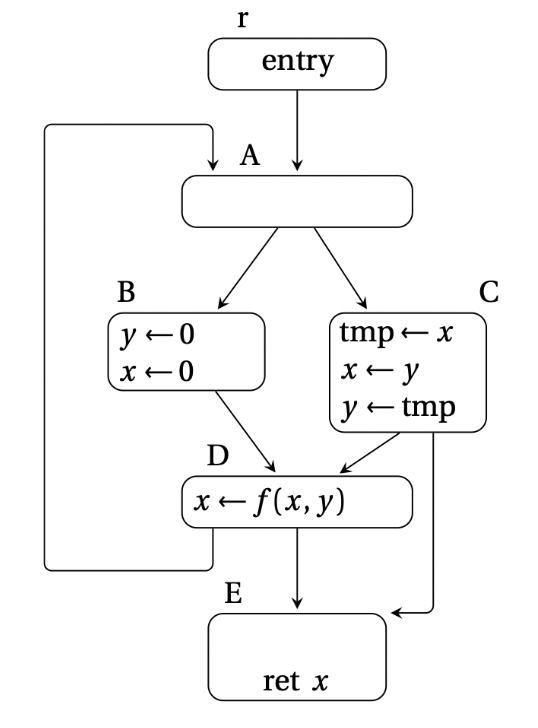
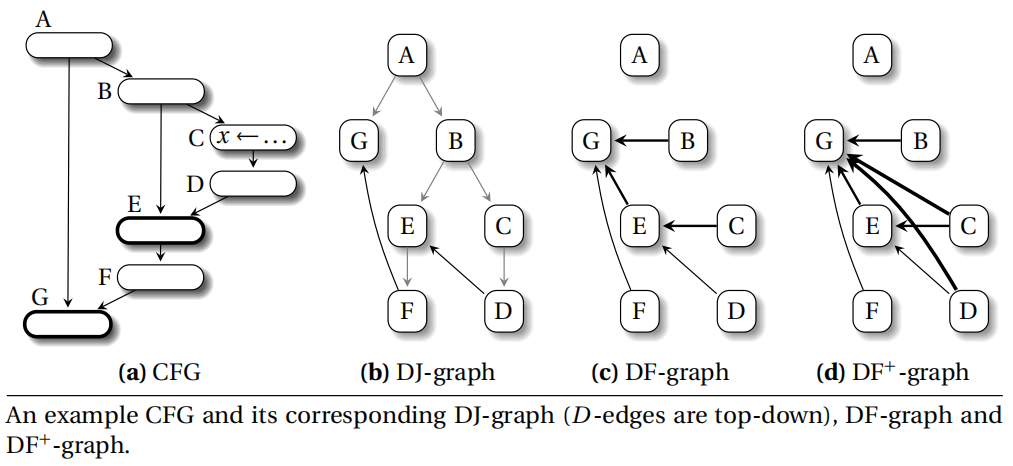
CFG，control-flow graph，控制流图，这张图会作为案例来进行讲解。

2、SSA 的构造

先解释下 live-range(存活区间)，即变量活跃(存活)时其处在的所有程序点(program point)的集合，range 代表的是一连串的指令。

构造 SSA 的算法主要有两个步骤：

  1. phi 指令的插入。采用存活区间传播(live-range splitting)的方法，来保证对变量的使用，只会有一个定义出现。
  2. 变量重命名。给每个存活区间(live-range)的变量赋予唯一的名字。

2.1、join set 并集

join set 由 join nodes 组成，这个节点代表的是，在不相交的路径上，两个或以上的不同元素到达的节点。

比如：join set({B，C}) = {D}，说明有不相交的路径可以从 B 到 D 和 从 C 到 D。

而在案例图中，join set({r，A，B，C，D，E}) = {A，D，E}，因为只有 A、D、E 有多条前继边。

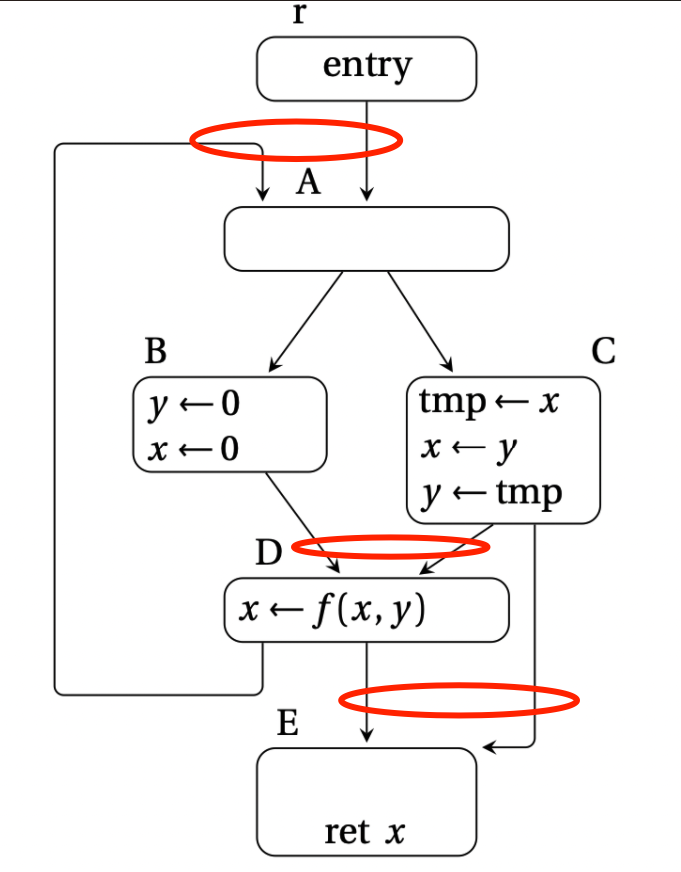
2.2、dominance frontier 支配边界

节点 n 的支配边界，简写为 DF(n)，是被节点 n 所支配的 CFG 域中的边界。

如果节点 x 支配节点 y 但 x != y，那么节点 x 严格支配(strictly dominate) 节点 y。

而如果节点 n 支配节点 x 的前继节点，但节点 n 不严格支配节点 x，那么 DF(n) 包含所有这样的节点 x。

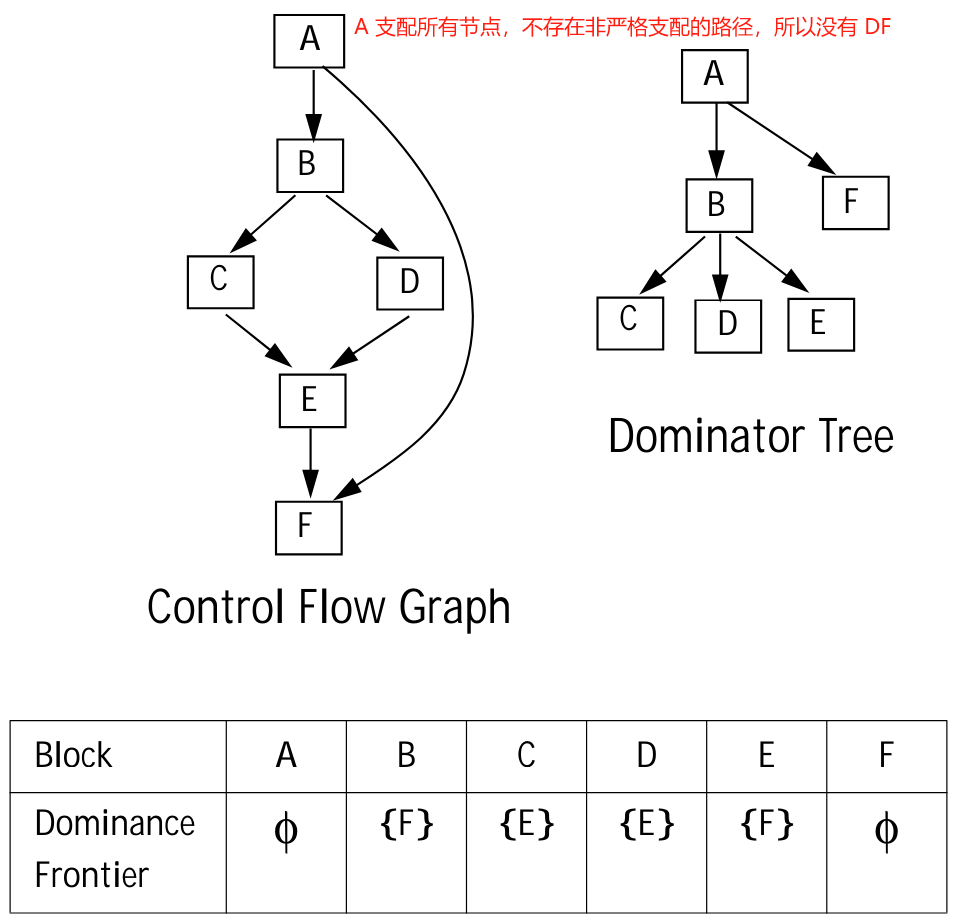
计算支配边界的算法需要用到 DJ-graph 的概念，是 CFG 的支配树，生成了 D-edges(dominance edges，表示支配关系的边) 和 J-edges(join edges，所有不会严格支配它的目标节点的 CFG 边)。还有 DF-edge(dominance frontier edge) 的概念，代表目标节点是源节点的支配边界的边。

DF+-graph 是加上了传递闭包，因为 C->E 和 E->G 是 DF-edge，所以直接补上 C->G 为 DF+-edge。所以在 C 的定义 x，会在 E 和 G 都插入 x 的 phi 指令。

计算支配边界的算法如下：

2.3、fixed point 不动点

根据维基百科的解释：在数学中，函数的不动点或定点是指被这个函数映射到其自身一个点。例如，定义在实数上的函数

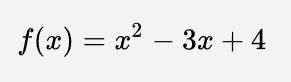
那么 2 是函数的一个不动点，因为 f(2) = 2。

也不是每一个函数都具有不动点。例如定义在实数上的函数 f(x) = x+1 就没有不动点。因为对于任意的实数，x 永远不会等于 x+1。用画图的话来说，不动点意味着点 (x,f(x)) 在直线 y = x 上，或者换句话说，函数 f 的图像与那根直线有共点。

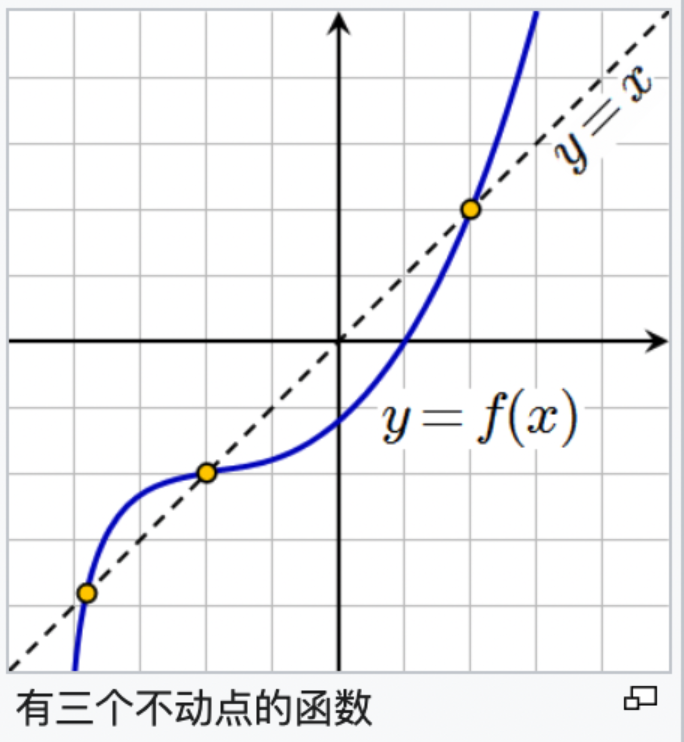
在函数的有限次迭代之后回到相同值的点叫做周期点；不动点是周期等于 1 的周期点。

2.4、phi 指令的插入

有了支配边界的概念，phi 指令的插入就直截了当得多了。

Defs(v) 代表包含有变量 v 定义的节点的集合，对于变量 v，我们可以遍历支配边界 DF(Defs(v)) 来插入 phi 指令。这样构造出来的 SSA 本身就带有支配的属性了。

再拿案例图分析，Defs(x) = {B，C，D}，而 DF(Defs(x)) = {A，D，E}，因此把关于 x 的 phi 指令放在 A, D, E 节点的开头。

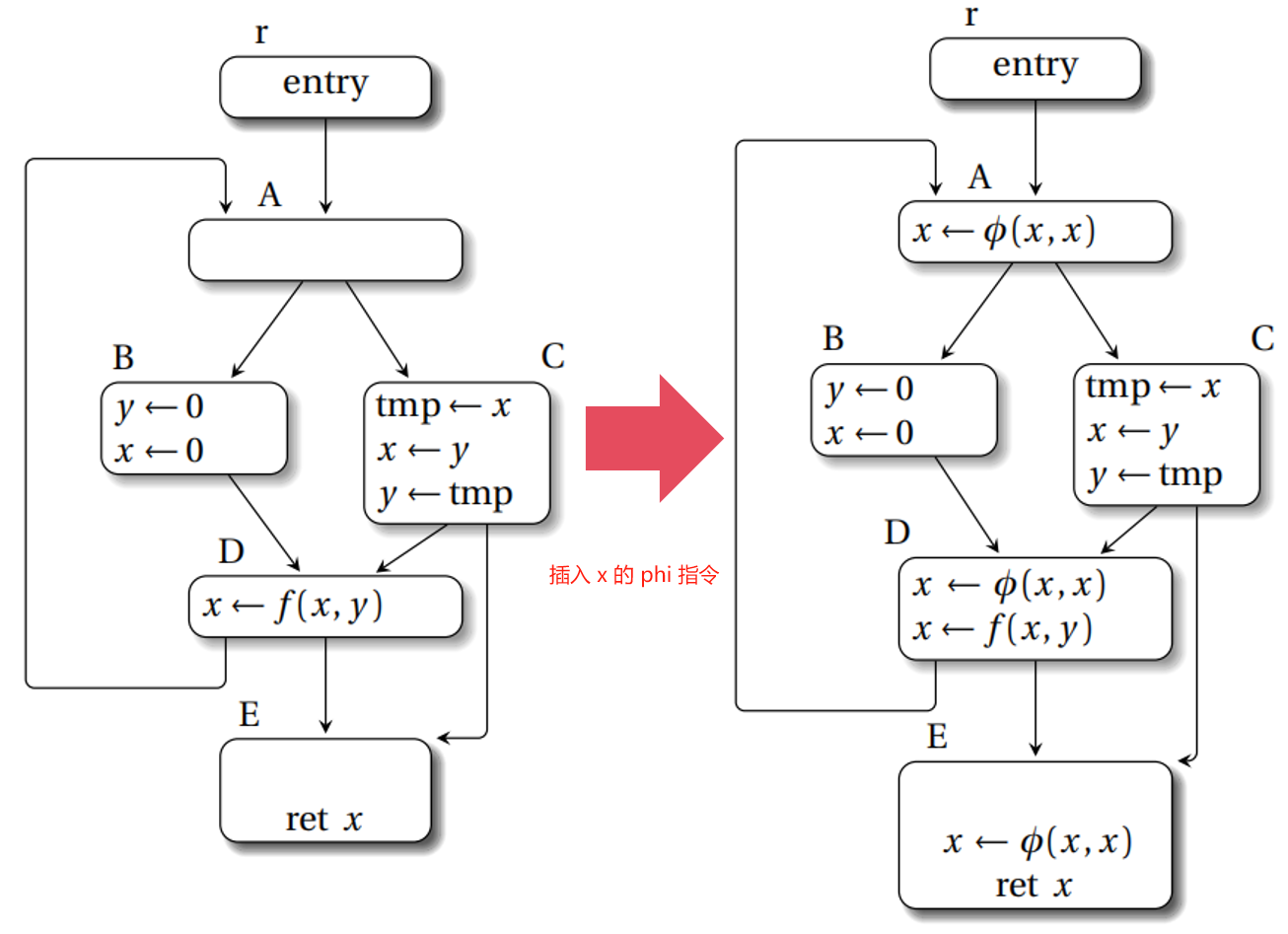
这里再以一张图展示 phi 指令插入的算法：

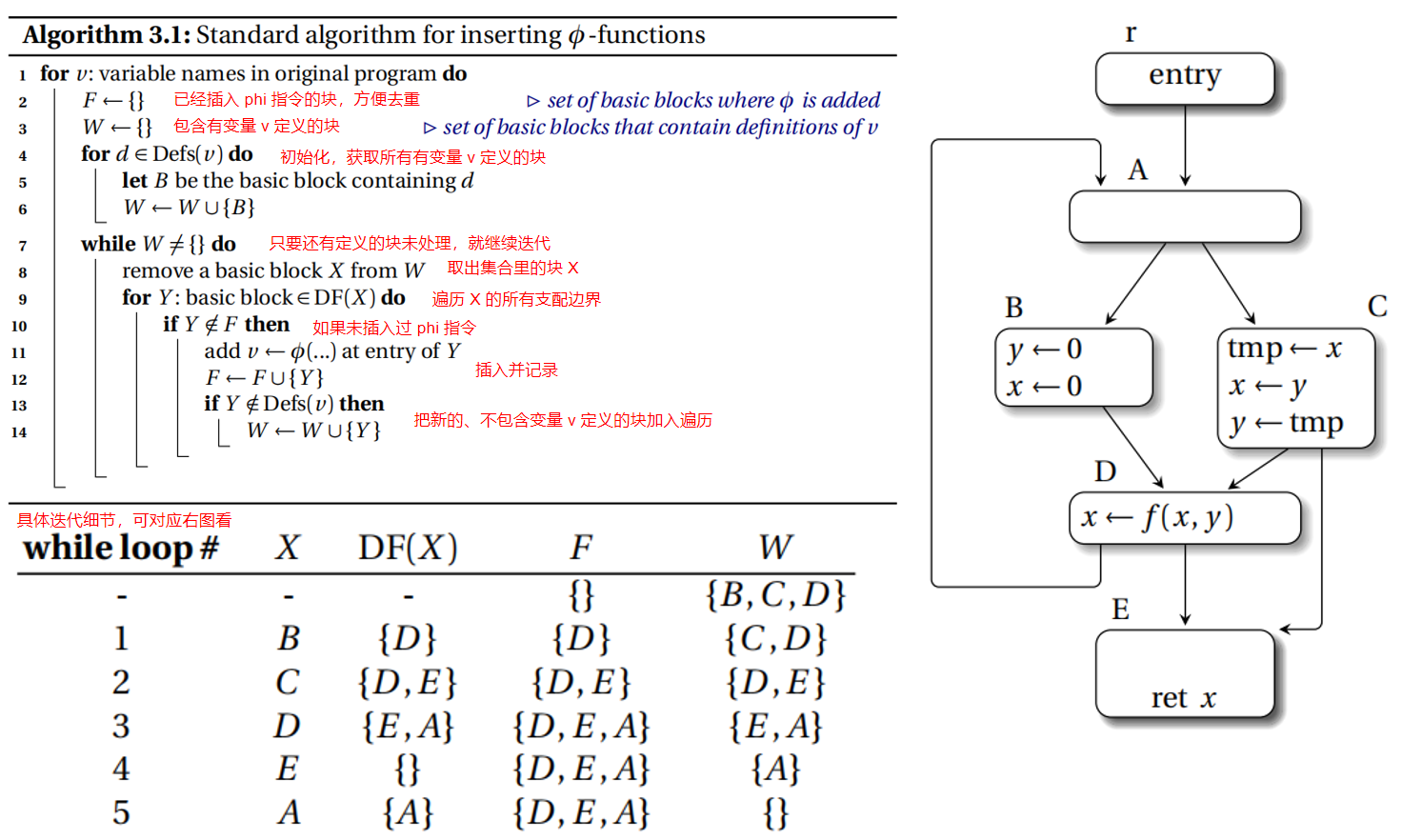
2.5、Variable renaming 变量重命名

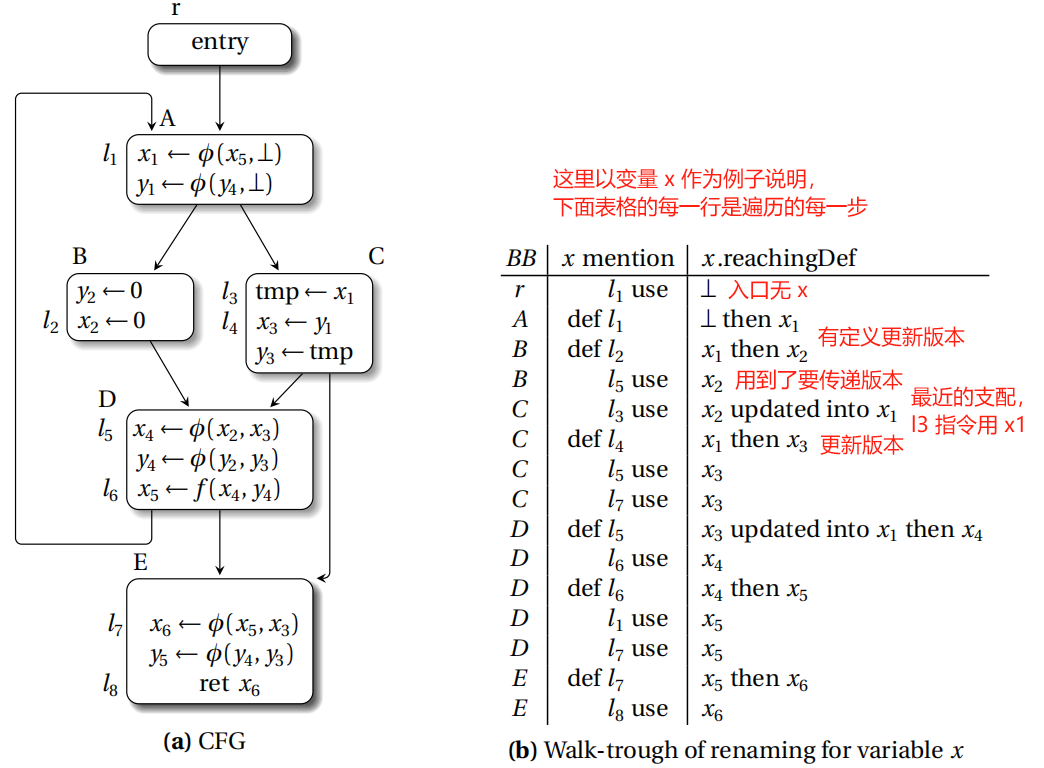
由于 phi 指令的插入把变量的 live-range 分割开了，变量重命名就把这些新的独立的 live-range 赋予新的变量名，也称之为变量的版本。

算法可以粗暴地深度遍历支配树来实现：

本文对应案例如下：

3、SSA 的析构

转化成 SSA 格式是为了可以更容易地实现分析和优化，而在优化过后，要生成代码了，就需要移除 phi 指令了，因为这是 SSA 特有的，所以要进行 SSA 的析构。

一种简单直接的方法是，把所有与 phi 函数相关的变量都重命名为一个唯一的变量，然后其操作数应该就具有相同的名称了，因此可以进行删除且合并相关的 live-range。

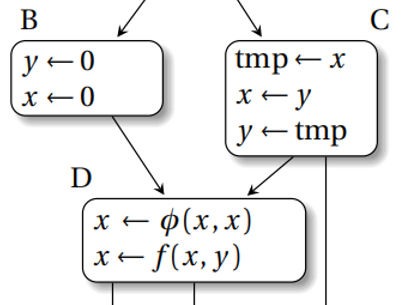
我们把 phi 相关的这些变量组成一个 phi-web，可以使用并查集来实现。

一般移除 phi 函数直接把 phi 函数还原到前继是最简单的。

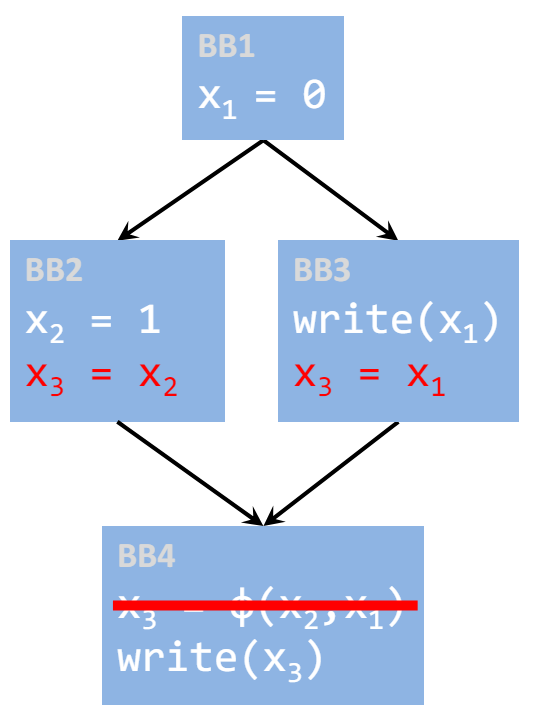
但还有复杂的情况，这里析构需要分割所有的关键边(critical edges，起点有很多后继节点 successors，而终点有很多前继节点 predecessors 的边)，然后在其前继节点的末尾用拷贝操作来替换掉 phi 函数。

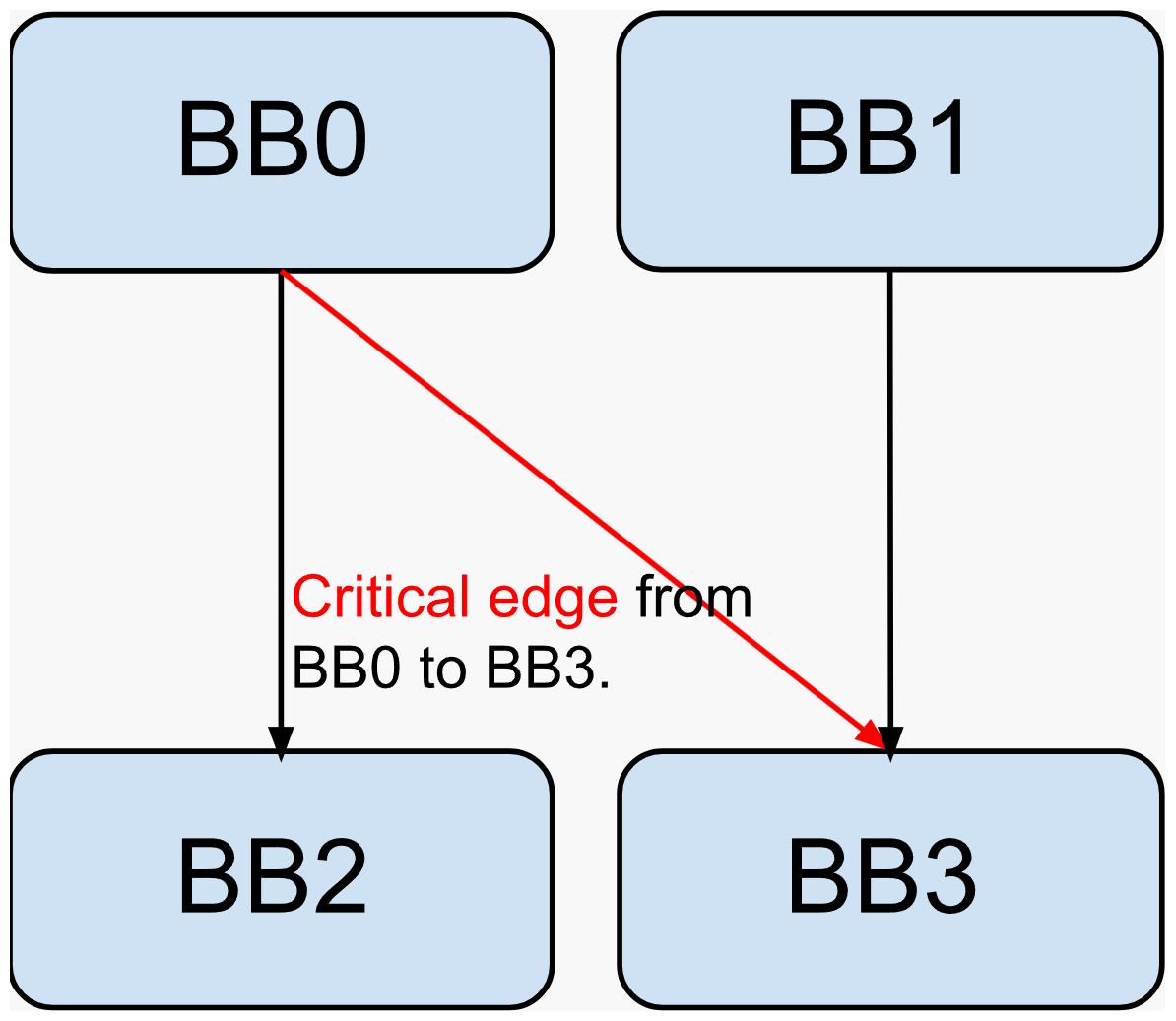
对于关键边，把 phi 函数直接拆到它们的前继是不对的，因为会影响它们前继的其它后继节点，所以解决方法是在关键边加入空块来写。

因为一个基本块里的所有 phi 指令是并行同时执行的，我们的拷贝也需要保证同时执行。

参考