SSA: 简化编译器优化的格式
文章目录
最近在看《Static Single Assignment Book》这本书,做了些笔记,简单介绍下对编译器优化非常重要的 SSA 格式。
1、SSA 的概念
SSA (static single assignment),是 IR (intermediate representation,中间表示)的一种表现形式。
- static:代表对静态的代码文本的分析。
- single:代表变量定义的唯一性。
- assignment:代表变量赋值。
SSA 意思是在静态代码中,每个变量只会被赋值一次。SSA 是静态的单次定义,并非运行时的,所以处于 for 循环中的变量并不影响。
1.1、用处
SSA 主要用在 gcc、llvm 等编译器的数据流分析。SSA 还被使用在 JIT 字节码当中(java bytecode、llvm bitcode),因为它能简化算法。
一些高级语言可以开启 SSA 的能力,主要利用了其变量的不变性从而简化了并发的复杂度,能够解决并发当中数据依赖的问题。
这里用简单的代码说明一下 SSA 的优势:
|
|
错误的分析可能会认为这里的 y 和 z 是相等的,因为它们有一样的定义赋值 (x+1)。但 x 的值取决于它所处的位置,依赖于上下文,所以这里并不相等。
|
|
如果转成 SSA,就清晰了,现在只有 x1 和 x2 相等,y 和 z 才可能相等。
1.2、转换方式
SSA 的构造步骤: 第一步是放置 φ 指令,第二步是重命名变量。
一个是为了处理不同分支合并时的结果计算,一个是为了保证变量定义的唯一性。重命名一般是给变量增加下标来完成的,像上面代码中的 x1 和 x2。
1.2.1、phi 指令 φ
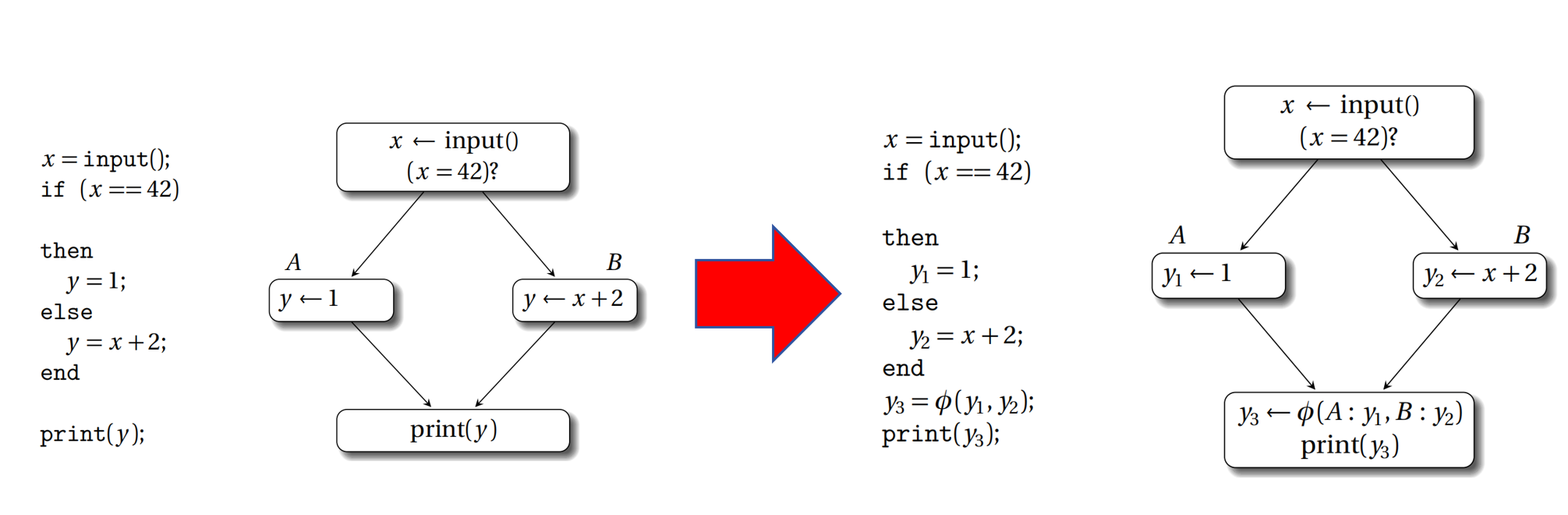
φ 指令是为了在控制流入边的合并处(merge point),从不同的入边合并值,用来根据控制流的路径动态选择所需的值。
当编译器将上图左边代码转换成 SSA 形式,在合并处会同时出现两个变量,需要根据条件判断的结果来选取值。
这里的 phi 指令代表,如果执行控制流(executed control-flow)从基本块 A 来就选取 y1 的值,从基本块 B 来就选取 y2 的值。
一个重点是:如果一个 Basic Block 的开头有多个 φ 指令,那么它们是同时并行执行的,而非串行。
这点很重要,因为当一个 phi 指令的目标(左侧变量),和另一个 phi 指令的输入(右侧变量)是相同的话,并行与串行的结果是不一样的,可能的案例是复制传播优化的结果。
φ 指令会在生成程序文件或执行时被移除,通常只用在程序的静态分析。
1.3、与传统 data-flow 分析对比
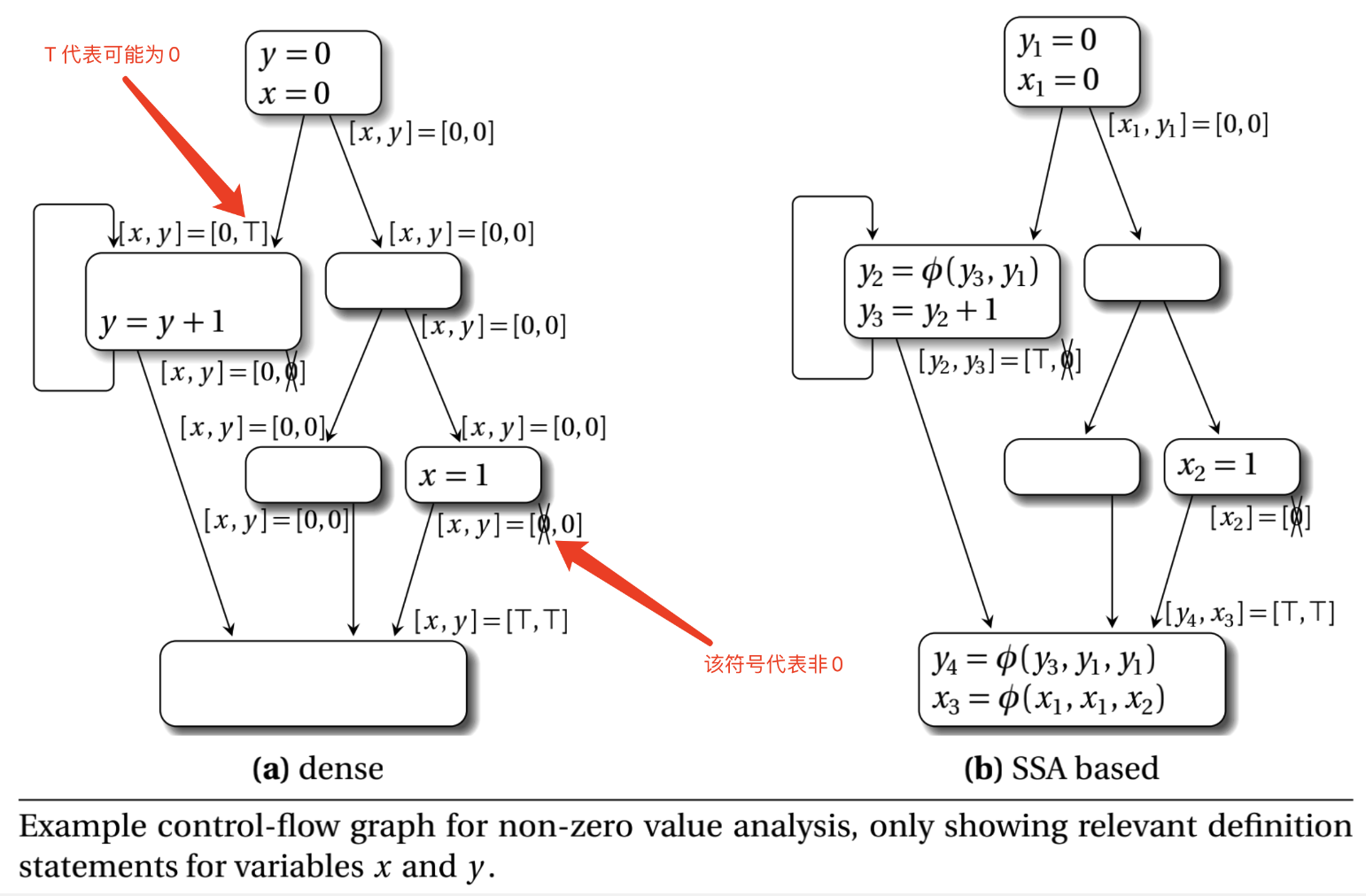
在进行 Data-flow 分析的时候,需要在编译时收集相关信息。上图是非零值分析的案例,需要分析变量是否为 0 或 null。
转换成上图中右边 SSA 形式后,就不需要在每个程序点(program point)收集全部的变量信息,只需要判断它的定义处即可(def-use links),而且对于分析的结果而言会更加简洁。
1.4、优点
SSA 主要有以下几个优点:
- 编译时间更少(Compile time benefit)。如上面展示过的图,SSA 中变量的引用关系更加清晰,不用在程序点(program point)检查所有变量。
- 有利于编译器的开发(Compiler development benefit)。编写 SSA 版本的 pass 更加容易,有利于程序分析和转换。
- 执行时间更少(Program runtime benefit)。由于 SSA 形式更简单,所以运行 pass 或程序分析需要的运行时间更少。
2、Def-use and use-def chains
Def-use chains are data structures that provide, for the single definition of a variable, the set of all its uses.
In turn, a use-def chain, which under SSA consists of a single name, uniquely specifies the definition that reaches the use.
DU 链代表变量的定义到所有使用它的集合,UD 链代表唯一指定了使用者到变量的定义。用来做分析和优化的辅助信息非常重要,但通常会需要保存和更新大量的信息。
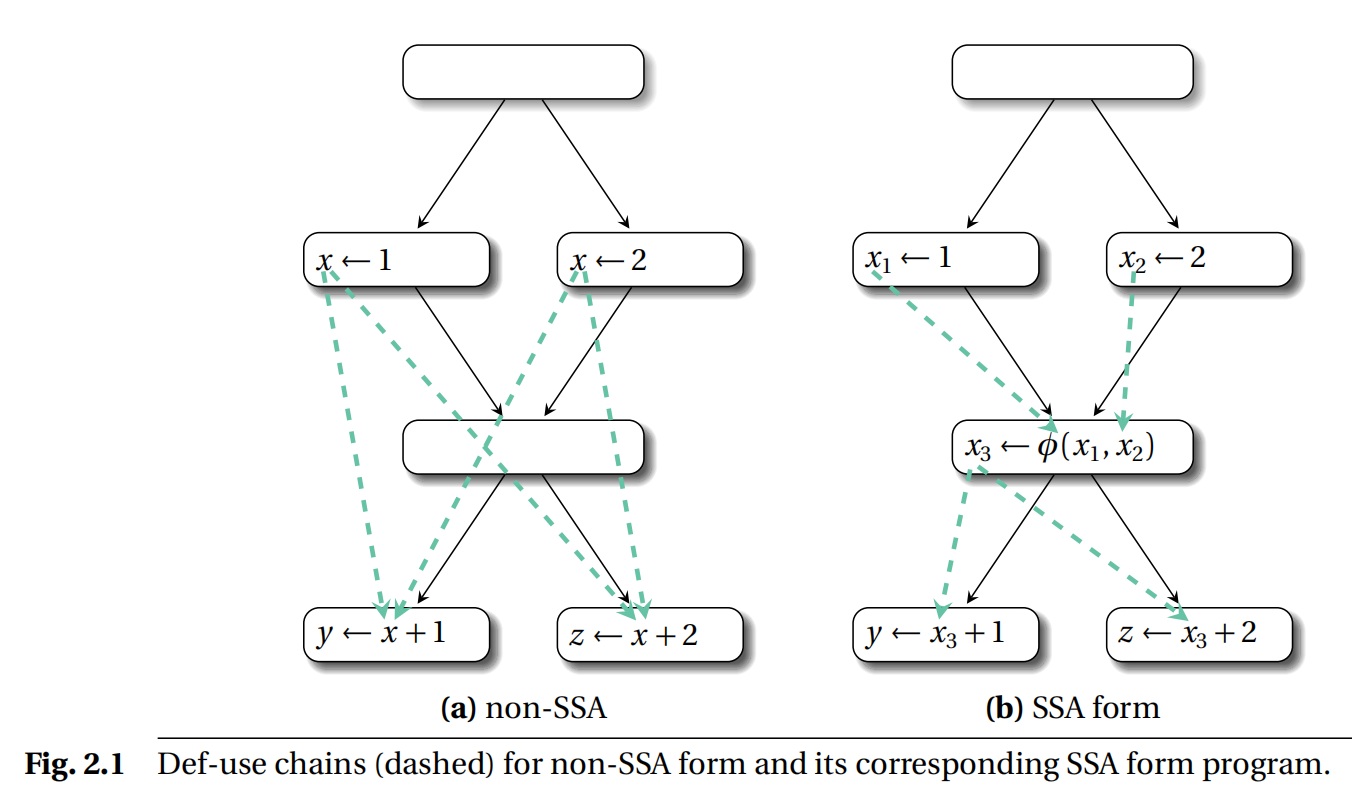
SSA 格式大大简化了 DU 链,因为能够更早地整合数据流信息。SSA 由于每个变量只能有一个定义,所以对于维护 UD 链比较方便容易,还使得 DU 链和 UD 链可以互相反推。
3、SSA 相关概念
3.1、strict(dominate)
从 entry 到 exit 的每条路径上,如果每个变量在被使用前都已经定义了,则称为 strict(严格)。
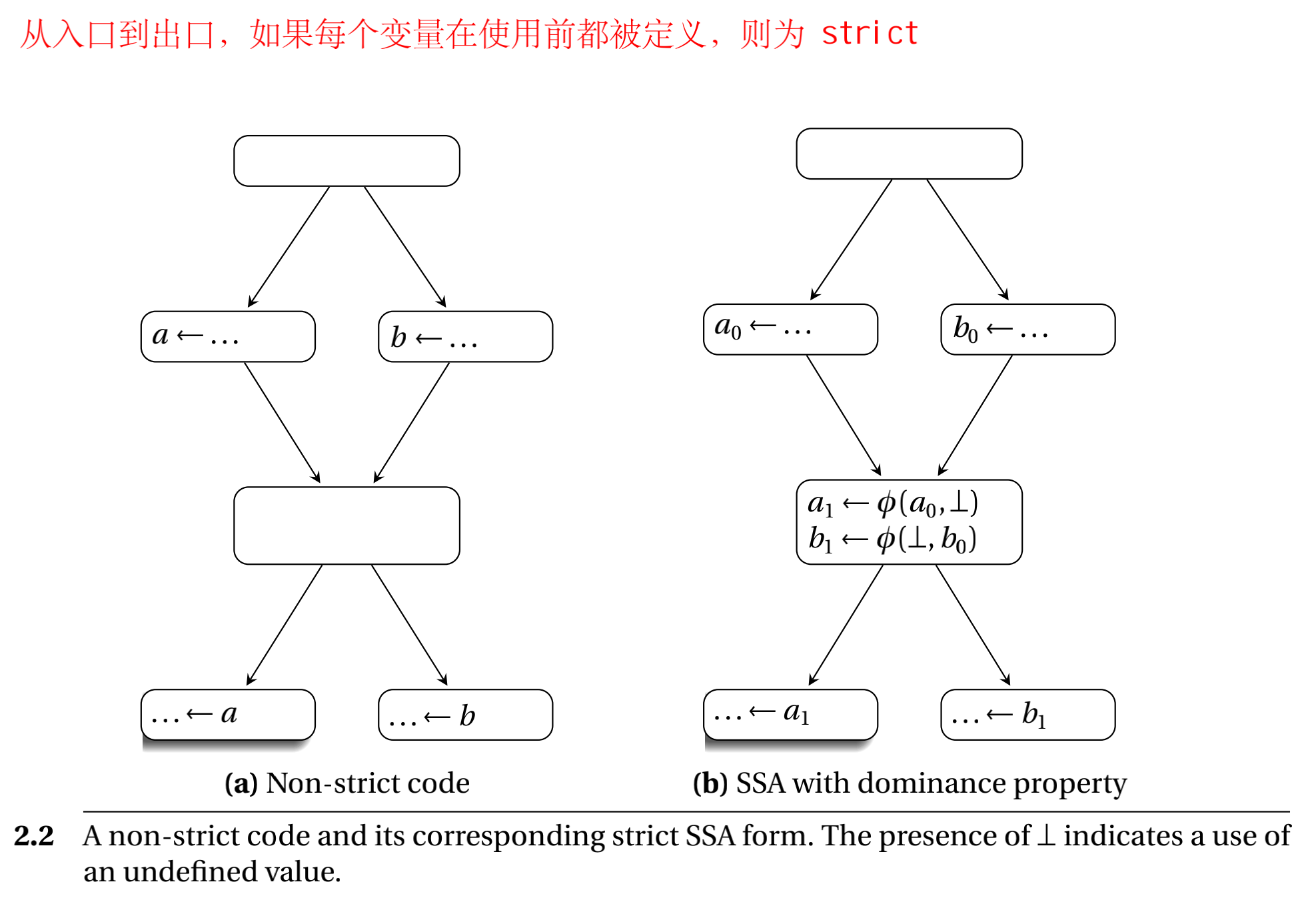
在图中左边,我们可以找出某条路径,使用了变量 a,但并没有定义变量 a,所以我们称其为不严格的。而在右图中,由于在汇集处,采用 phi 指令定义了 a1 和 b1,所以无论哪条路径,在变量使用前都进行了定义,称之为严格的。
通常不严格的路径,在某些语言是允许的,但也意味着可能程序存在逻辑错误。如果把所有变量都写在程序入口点(entry point),那就能保证是严格的。
为了保证严格性(strict SSA form),就会插入 phi 指令来实现。但并不会改变程序的语义信息,使用未定义变量的错误还是会出现,因为它使用的是隐式的伪定义(implicit pseudo-definition)。
3.2、支配 dominate
在 SSA 中,strict 也被称为 dominance property(支配属性),变量的 use 被 definition 所支配。
在 CFG 中,若从程序入口点(entry point) 到 basic block n2 的每条路径上,都有 basic block n1,则称 n1 支配 n2。每个节点都支配它自己。
支配符号:n1 dom n2
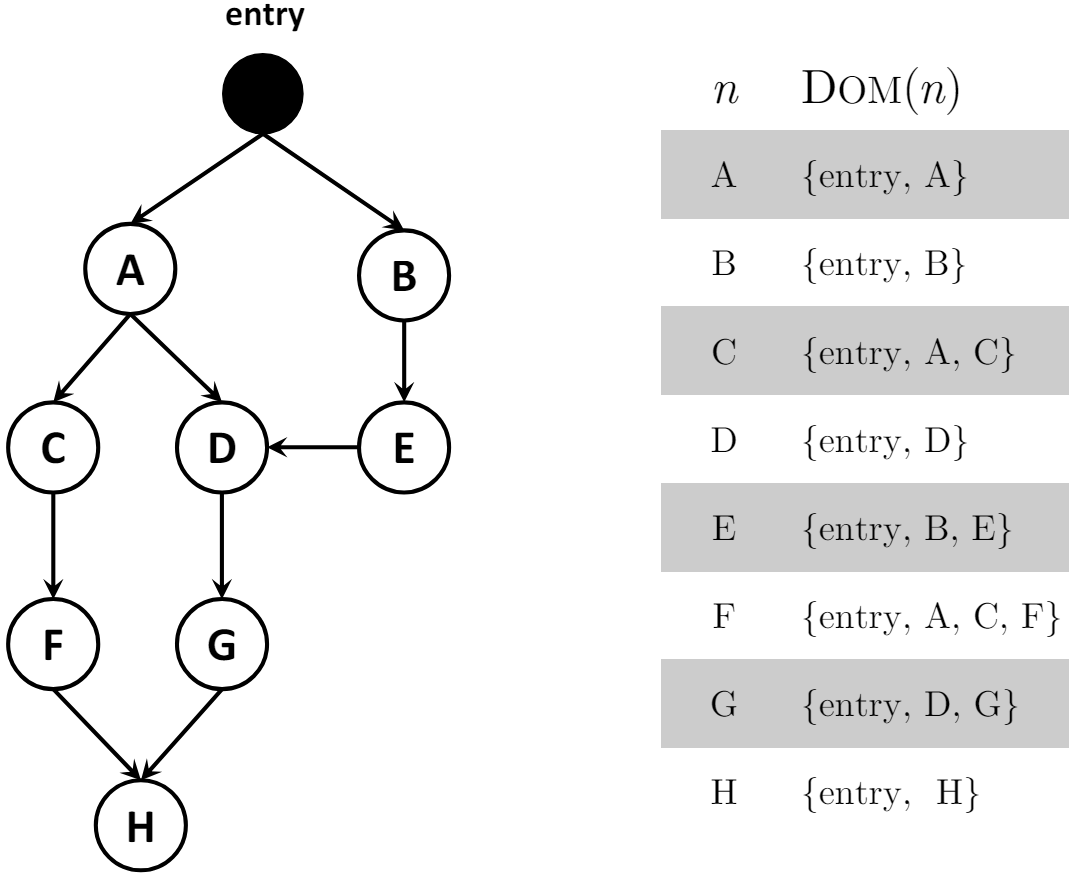
3.3、严格支配 strictly dominate
在上述支配的基础上,如果 n1 支配 n2,但是 n1 不等于 n2,则称 n1 严格支配 n2。
严格支配:支配且不相等。 (因为变量可能在同一个基本块定义和使用,需要区分)
严格支配符号:n1 sdom n2
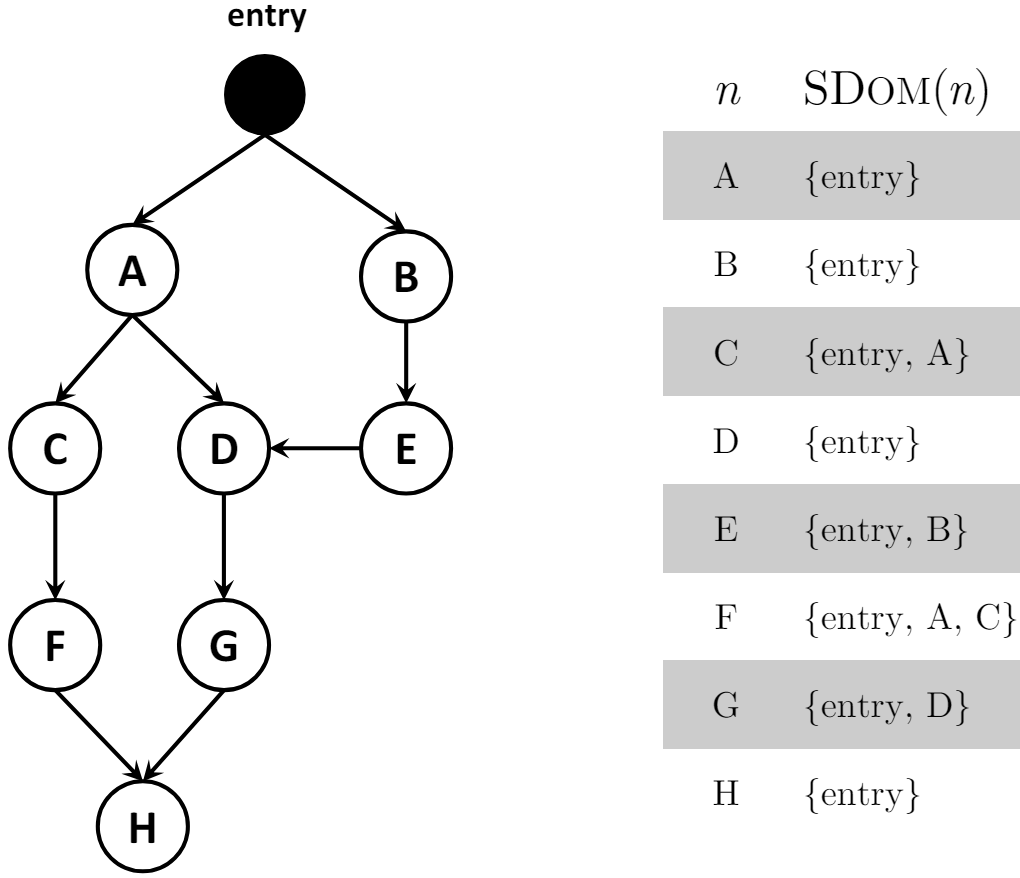
3.4、直接支配 immediately dominate
直接支配:一个唯一的节点,它严格支配 N,但不严格支配 { 其他严格支配 N 的节点 }。它是 N 的最近的一个严格支配节点。所以除了 entry 节点外,其他节点都有直接支配属性。
The immediate dominator or “idom” of a node N is the unique node that strictly dominates N but does not strictly dominate any other node that strictly dominates N
直接支配符号:n1 idom n2
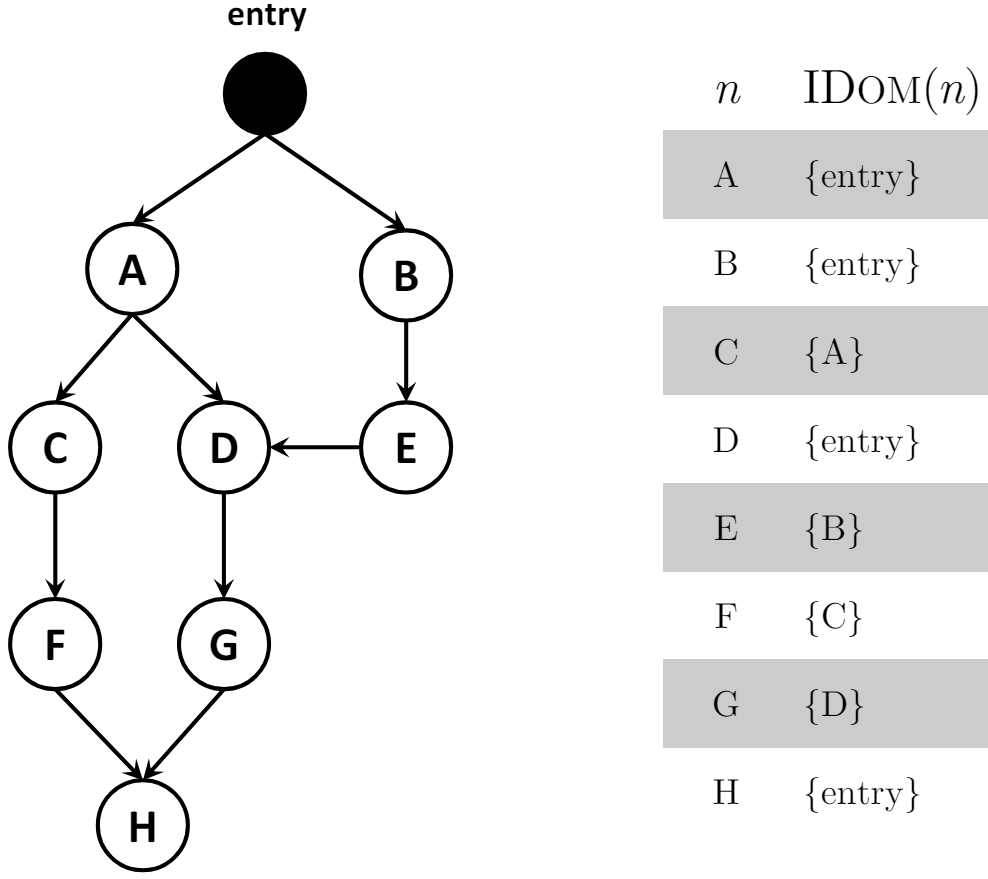
在支配树(dominator tree)中,每个节点的孩子,就是该节点直接支配的点。依据这个特性,我们可以设计一个快速而又高效的算法,来判断变量在某个程序点是否存活(live),判断两个变量是否有交集(interfere)。
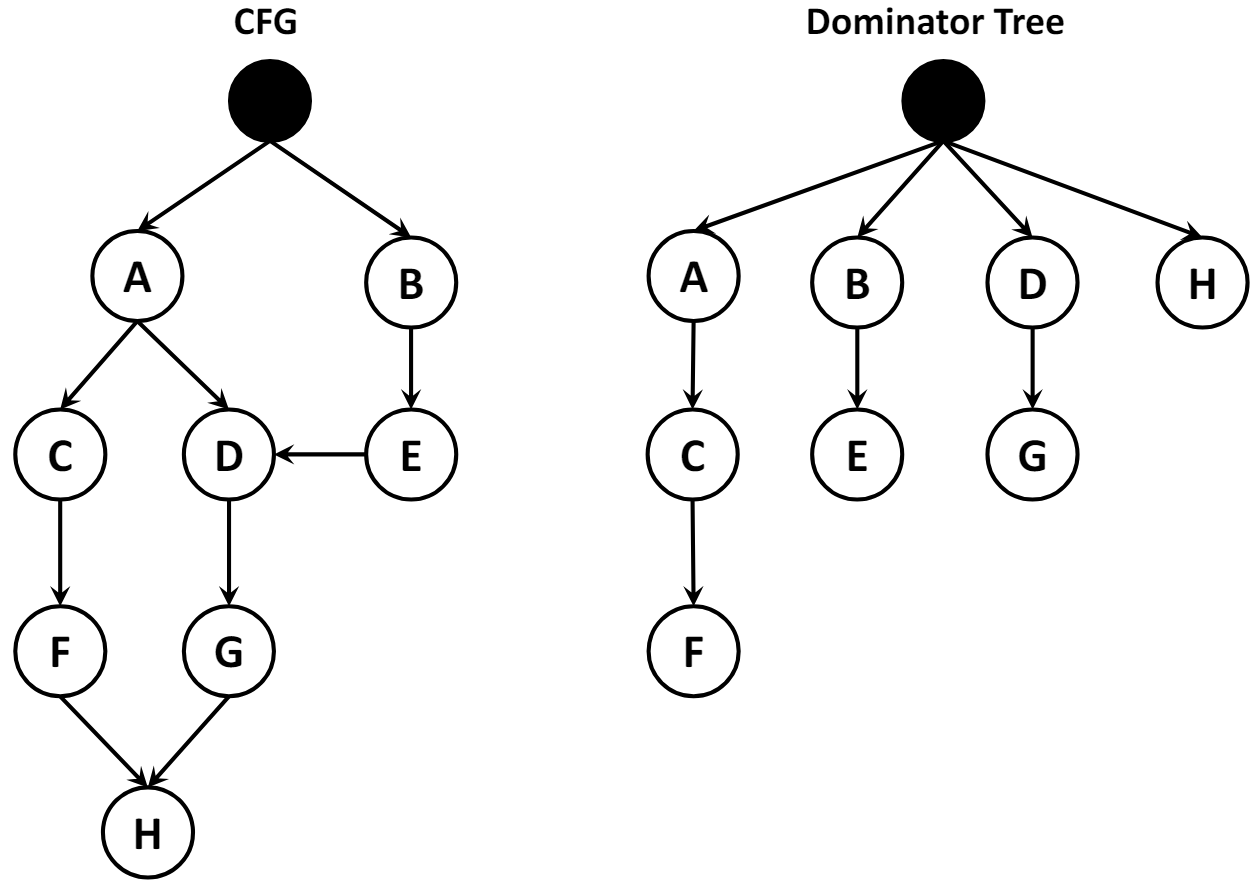
还有一个好处就是可以很好地解决寄存器的分配问题:对于存活范围(live-range)的交集图(intersection graph),称之为弦图(chordal graph)。弦图对于解决 NP 难问题,可以有线性时间解,包括图染色问题。图染色问题对于寄存器分配操作是很重要的,寄存器分配可以表示等价为交集图的染色问题。在图中,如果两个变量有交集,即有连边,说明它们不能被分配到同一个寄存器中。而弦图能够很好地简化了这个难题。
3.5、格(Lattice)
-
偏序集合:格建立在偏序集合的基础上。一个偏序集合是由一个集合 S 和一个偏序关系 ≤ 组成的,记作 (S,≤)。偏序关系满足自反性(对于任意 a ∈ S,有 a≤a)、反对称性(若 a≤b 且
b≤a,则 a=b)和传递性(若 a≤b 且 b≤c,则 a≤c)。 这里描述的是抽象的概念,并不代表实际,比如可以把类的继承关系看作是一种偏序关系。 -
格的定义:在偏序集合 (S,≤) 中,如果对于任意两个元素
a,b∈S,都存在唯一的最大下界(下确界,记作 a∧b,与操作)和最小上界(上确界,记作 a∨b,或操作),那么这个偏序集合就称为一个格。
4、SSA 的转换
4.1、minimal SSA
为了满足 SSA 变量单次赋值的特性,一般用在程序点汇集之处(join set),插入最少数量 phi 指令来保证这一行为。这个 minimal SSA 是在插入 phi 函数之后,而在变量重命名之前所形成的。
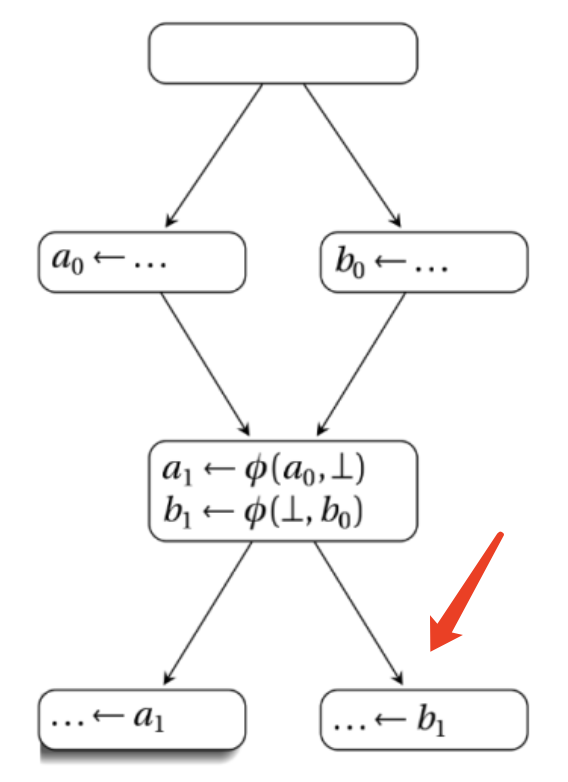
但它为变量插入的 phi 指令,其变量在某条路径上并不一定存在。像图中的一样,插入了 a1 <- phi(a0, 空),当使用 b1 路径时,这条 a1 的 phi 指令是冗余的,导致这个 phi 指令是没有必要的,因为很多分析和优化只关心变量在哪是存活的(live)。
4.2、pruned SSA
在构造 SSA 之前,先进行存活分析,不构造没必要的 phi 指令;或者先生成 minimal SSA,再去掉没必要的 phi 指令,则构造成 pruned SSA。
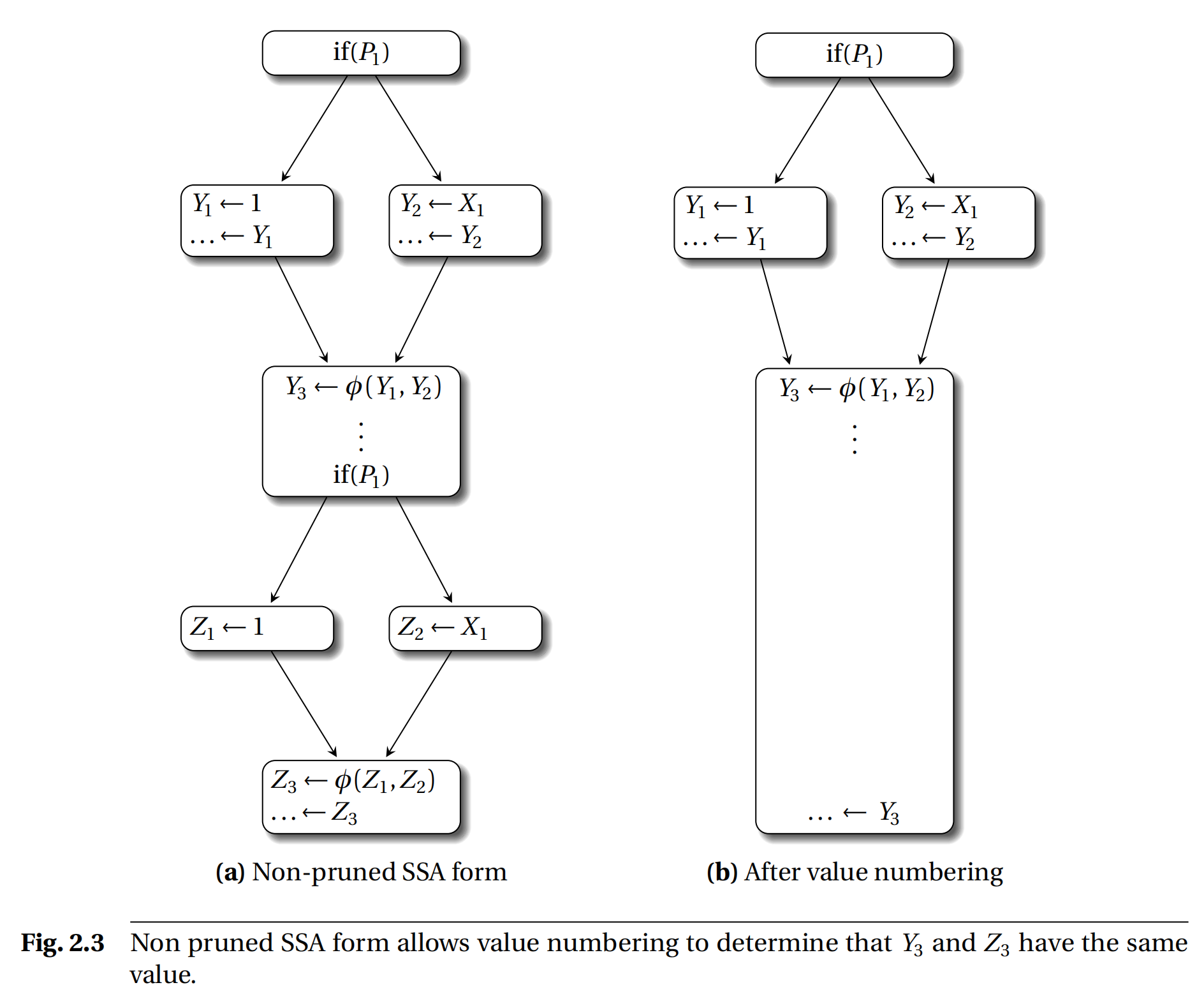
这里图中左边为 minimal SSA,右边为 pruned SSA。Z3 和 Y3 实际为重复操作,所以被去掉了。
4.3、transformed SSA
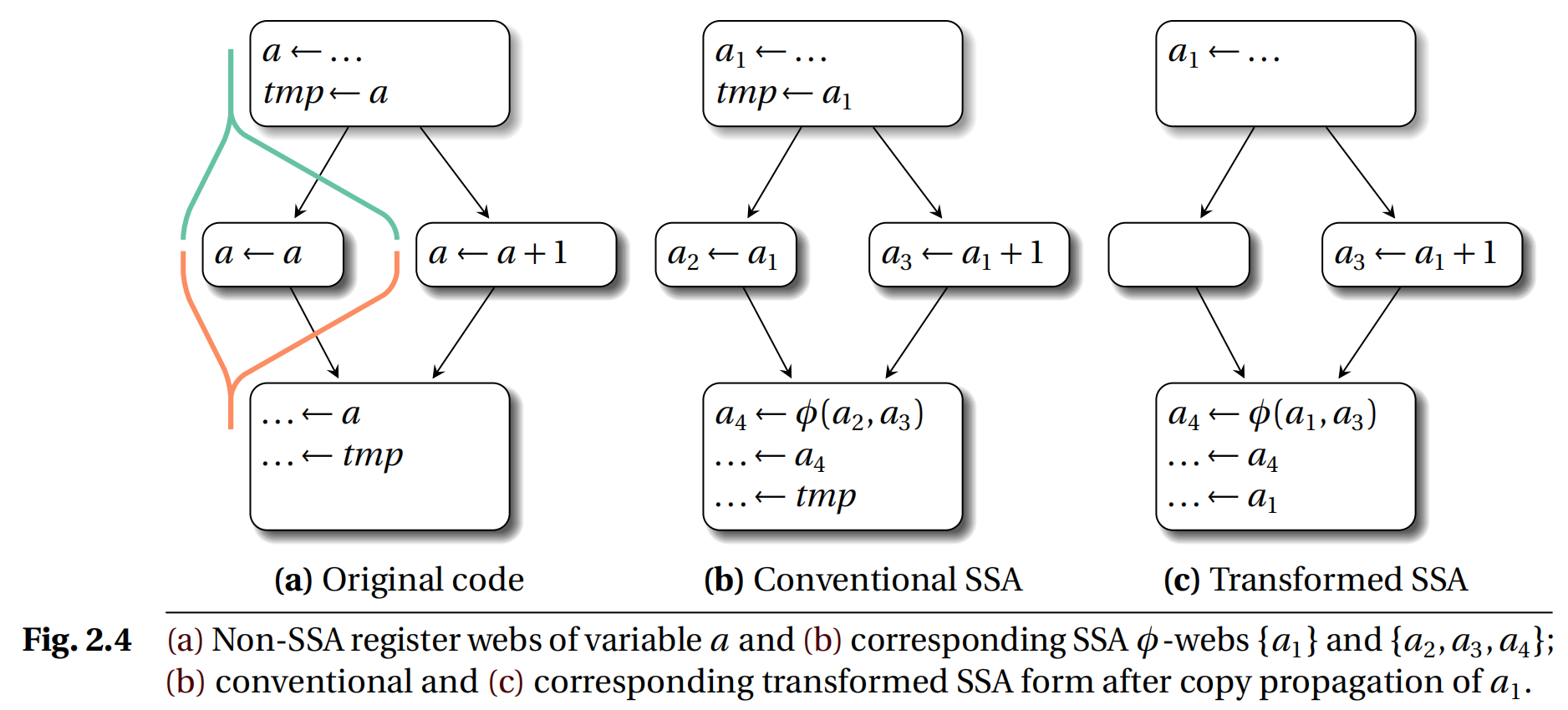
在这里,一个 web 称之为 DU 链的最大合集,它们有共同的 use 或 def。在上图(a)中,这里有对于变量 a 的两个 web。转换成 minimal SSA 重命名这些 web 的变量名。而 phi-web 就是同一个 phi 指令所影响到的变量链路合集。
传统的 SSA(Conventional SSA,C-SSA)对于 phi-web 的交集并不敏感,如图中的变量 a,通常优化器会把 C-SSA 再转换成 Transformed SSA(T-SSA),这样就可以识别到一些变量其实是属于同一个 phi 指令的,比如图中的 a1 是其中的一个交集。
参考
文章作者 calssion
上次更新 2025-04-30